MathPuzzle.com

Mathematica 7 launches: Mathematica 7 has launched, as noted in Stephen Wolfram's blog post. Among the new features are huge equation typesetting, transcendental roots, and discrete calculus. Looking back at the version 6 discussion, it's perhaps inevitable that comparisons will be made to CAR, CGsuite, GAP, Geogebra, Geometer's Sketchpad, Geometry Expressions, Geonext, LaTeX, Magma, Maple, Matlab, nauty, noneuclid, Pari, Sage, or SeifertView. In other news, the Wolfram Demonstrations project now has over 4000 interactive math demos.

CAs on XKCD: And about the same time, cellular automate were used in webcomic XKCD.
More Demonstrations: Some of the newer demos are Complex Newton's Map, Wire and String Puzzles, and Social Golfer Problem.

La Ora Stelo: Irrational tiling systems have the property that for a sufficiently large room, it can be tiled almost perfectly without any of the tiles needing to be cut. It's very tricky to make a nice puzzle out of this, because they quickly become human-insolvable. For example, I consider that one of my own worst puzzles is the 14 Tridrafters, due to the rarity and nonintuitiveness of the solutions. To my surprise, it turns out that the Golden Triangles are "nice" for human solvers.

Jacques Ferroul seems to be the first to make a polyform set out of the golden triangle and golden gnomon, which has 2 shapes at order 1, 8 shapes at order 2, and 22 shapes at order 3. Add 5 more triangles to increase solvability, and a perfect pentagon is possible. The solving area is etched with 8 more perfect pentagons of different areas to solve. Jacques calls them the Polyore, and it impressed Kate Jones enough that it is now available for sale at Kadon Enterprise. There, an extra page on polyore is available. Jacques has put together another 8 pages of material. In addition, he is offering a pair of $150 prizes, with no purchase necessary. Recall I mentioned irrational tiling systems? Jacques has identified 148 possible trapeziums that might be solvable with the basic or extended set, and will award a prize to whoever solves the most of them. I'm not sure how well computers will do with these, since there is a fractal nature to how the shapes behave. I bought a set, and it's my favorite puzzle purchase of the year. In addition to all the nice math behind it, it's gorgeous, too. Also at gamepuzzle, large solutions.

Mathematical Coloring Book: Alexander Soifer, a former professor of mine, my reason for having Erdos number 2, and the editor of Geombinatorics, has finished his long-time work The Mathematical Coloring Book. The book covers many aspects of mathematical coloring. For example, what is the chromatic number of the plane? In the book, I show that 1/302th of the plane can be removed, and a unit six coloring is possible. All the thick bars have unit length. The x value is the first real root of 1 - 40x + 448 x² - 720x³ - 11288x⁴ + 38048x⁵ + 88576x⁶ - 491328x⁷ + 391824x⁸ +1082624x⁹ - 2217984x¹⁰ + 231424x¹¹ + 3368960x¹² - 4374528x¹³ + 2490368x¹⁴ - 655360x¹⁵ + 65536x¹⁶.

Periodic Table Element Cards: Theo Gray, of Popular Science, Mathematica, and periodictable.com fame, has made the ultimate element card deck. He's also made an element jigsaw puzzle. They are large enough to cover a wall, or an innocent passerby.

New Puzzles by Erich Friedman: Erich has published a number of great new puzzles, including: 23maze, plustimes, letterorder, trios, duplicate, insert, and anagram. For his December Math Magic, Erich is looking at graphs with numbered vertices, where each vertex is the sum of digits in adjacent vertices. The Math Magic Archives are looking increasingly spectacular.
Pictures of Mathematicians: The Dubner Library has collected several hundred pictures of famous mathematicians for maa.org.
FBI 100th Anniversery: For the 100th anniversary of the FBI, Dylan Bruno of Numb3rs gave a congratulatory message.
Surf: Surf is a nice program for algebraic surfaces.
Math Humor on the Komplex Plane: Travis has collected various pieces of math humor for The Komplex Plane.
A Cube, in Phonecam Magic: The tricks behind a Phone Cam Magic video does nice trickery with a white cube.
Musical Road: By using grooves to induce sound waves, a musical road has been made.
Puzzle Design Competition and Puzzle Palace: The results of 2008 and the rules for 2009 for the Nob Yoshigahara Puzzle Design Competition are available. One of the winners is Vesa Timonen's Tangerine puzzle. George Miller has put several of these puzzles on his site: Ringworld (Oskar), TriGears (Oskar), Rainbones (Knuth), and Perfect Packing (Knuth).
New Cast Puzzle: A new Cast Puzzle is available: the Cast Equa. Another superb design by Oskar van Deventer.

23 Mathematical Challenges: DARPA released a list of 23 Mathematical Challenges that they will provide major funding for. CNN did the article DARPA Mathematical Challenges, and they used a graphic of mine for the Riemann Hypothesis (challenge 19).
Slashdot math Articles: Slashdot has had several nice mathematical items. First, an AMS article on formal proofs (Science News and Slashdot). Second, a Science News article on Knot Theory (and Slashdot). Third, a Science News article on the card shuffling of Persi Diaconis.
More on Theseus and other iTunes Puzzles: Jason Fieldman has put Theseus and the Minotaur on the iPhone, as mentioned at logicmazes.com. There is also an iPhone Puzzle blog, now, by Michael Cysouw. Subway Shuffle, by Bob Hearn, is another nice app. (But I don't actually have an iPhone, yet).
Stocks Update: Several asked me how my venture into the stock market is doing. I mostly went into electrical utilities with good dividends, good cash flow, and no debt. After a great week, I'm down 5% two months after getting in. I've made novice mistakes, so I'm practicing more with a no-real-money account on fool.com.
Automating a series of 3D figure in PovRay: Bob Harris: I've recently posted a simple example of how I automate the drawing of polycube packing solutions, including a couple python programs I wrote to control povray (povray does the actual rendering).
A Lifetime of Puzzles: A new book honoring Martin Gardner is available: A Lifetime of Puzzles. Various fans of Martin contributed articles, including Colm Mulcahy, Persi Diaconis, Ron Graham, Jerry Slocum, David Singmaster, Roger Penrose, Oskar van Deventer, Rik van Grol, Peter Winkler, Stewart Coffin, Frans de Vreugd, David Klarner, Ken Knowlton, Raymond Smullyan, Jeremiah Farrell, James Randi, Solomon Golomb, Dick Hess, Bill Gosper, David Wolfe, me, and Martin Gardner himself.
Optimal 25-mark Ruler: The 25-mark Golomb Ruler has been proven by distributed.net. It proves the 1984 result by Atkinson and Hassenklover (my related column). (Slashdot entry)
Twisted Grid: Here's some very twisted graph paper.
Extreme Rock Paper Scissors: I haven't worked out the full graph, but the 25 possibilities can each defeat 12 others in Extreme Rock Paper Scissors.
Scientist Behind Nobel Prize now a Courtesy Shuttle Driver: Douglas Prasher laid the groundwork for major research, when his funding ran out. So he passed it on to interested colleagues. They won the Nobel Prize in Chemistry.
Rotational Pentahex Oddity: Making a rotationally symmetric figure with a number of X pentahexes relatively prime to 6 has proven quite tricky. George Sicherman has managed to do it. He's added it to his Polyform Oddities page. He has also recently been exploring Baiocchi Figures for Polycubes.

Peter Grabarchuk Book, and Strimko: The Grabarchuk family has launched Strimko, a sudoku-related puzzle. Also, Modern Classic Puzzles is now out, by Peter Grabarchuk. I picked up a copy -- a very nice collection of 200 new puzzles. He's also made a new online puzzle, Untouchable 11. Put the 11 nets that fold into a cube into a 12x12 square so that no two nets touch each other.
Mobius Game: Mark Steere: This the first known game (at least by me) for a one-sided strip: Mobius. A filled board always produces exactly one winner. [Ed-Nice idea]

Will Shortz on the Simpsons: My friend for three decades Will Shortz will be a guest voice on the Simpsons tonight. It seems Lisa Simpson will become a big fan of crossword puzzles. Crossword composing master Merl Reagle will also lend his voice.
4000 Demonstrations: Now with 4000 math demos, the Education Portal, and new demonstrations on complex polynomials, drilling a hexagonal hole, powers of complex points, and exit times of Brownian motion.

PBS on Mandelbrot: Dick Saunders Jr: This is a good video on Mandelbrot fractals, etc. (North America only, sorry).
Viewmonster: I've been a fan of Lemon Demon for years now. In terms of favorites in my own playlist, he's the only one that beats Bach. Neil's latest album, Viewmonster, has been my favorite now for over a month now, bearing well even through my own harsh overplaying. I've been listening to music a lot lately.
Virginia Pegg (1944-2008): After a long illness, my mom died in her sleep on Sunday, November 1. She will be missed.

Buy Low, Sell High: Sorry about the recent lack of updates. First, there was a lot of support work for Numb3rs. There was a convention at Miami U. Then I started studying the stock market. Today, I'll use Scottrade for a few purchases, after using Yahoo Finance and Motley Fool for research. Some of the lessons I've learned... 1. There is never a rush to get in. 2. Have a watch list of companies you want to buy. 3. Be patient. Doing all the mathematical study has been perhaps a bit too fascinating.
Numb3rs: I just finished some work on the 11th episode. Our numb3rs.wolfram.com site has been expanded, and I'm doing a weekly math puzzle for CBS, at cbs.com/puzzle.
Demonstrations: In addition to the new Education Portal, Wolfram has been publishing lots of new Demonstrations, including some nice ones on the Golay Code, Voter Model, Nowhere Neat Squaring, Tetrads, 57-cell, Water-pouring Problem, Irreptiles, Galactohedra, 2-(64,8,1) Design, and Waterman Polyhedra. I've particularly been interested in the 57-cell. I believe it is the key for the 57-regular Moore Graph problem.

Tendry's Tales: I'm a huge fan of DROD, and they've just released their fourth major release, Tendry's Tales. I like it so far, but I'm not sure I like it more than Journey to Rooted Hold or The City Beneath, yet. Those two are my favorite games of all time.
Improved Pancake Sorting: You've got a stack of n pancakes of various sizes. How many flips with a spatula are needed to sort them? Thirty years ago, Bill Gates put down a bound for an answer. He's now been beaten, as explained in an article by Ivars Petersen, Improved Pancake Sorting.
4D Sudoku: I sent a puzzle email to the MathPuzzle Mailing List about the 4D Sudoku puzzle. Nyles Heise tried out the site. Nyles: "They have an on-line version of the puzzle as well as a handheld. Fortunately, I was able to be the first to solve the on-line version and was sent a complimentary hand-held version as the first solver. It is a very cool, very well designed gadget."
Adobe CS4: I did a long study of vector software, and finally decided on Adobe Illustrator and Wolfram Mathematica for my own purposes. I just got Adobe's latest upgrade. Downside: I had to clear away 20GB of space to install CS4. Yikes. Most of those were temp files I could then remove. So far, though, I'm liking CS4 a lot.

New Mersenne Primes: The next Mersenne exponents are 43,112,609 and 37,156,667. A Mersenne prime press release is available. And the MathWorld page is freshly updated.

Martin Gardner's New Mathematical Library

With help from Donald J. Albers, Gerald L. Alexanderson, John H. Conway, Richard K. Guy, Donald E. Knuth, and Peter L. Renz, Martin Gardner is releasing updated versions of his Mathematical Games columns. The New Martin Gardner Mathematical Library will soon be available from Cambridge. Hexaflexagons, Probability Paradoxes, and the Tower of Hanoi and Origami, Eleusis, and the Soma Cube are available for preorder at Amazon. Some copies are being given away free at the Cambridge Blog. Just solve the puzzle for a chance to win the book.

Will Shortz's KenKen Puzzle

Will Shortz has launched a new puzzle series called KenKen. KenKen 1, KenKen 2, KenKen 3 and a KenKen giftbook are available for October preorder at Amazon. Will made a video to introduce KenKen. Two more videos with Will Shortz were done by Forbes and Oprah. Some online puzzles are at the KenKen site. The original creator is Tetsuya Miyamoto.

Nested Klein Bottles

The photo of nested klein bottles at sciencemuseum.org.uk is worth a look.

Two Alphametics

Narasimhan Eswaran: Corals are made up of polyps and polyps make a coral. The first has two solutions, the second has a unique solution.

New Demonstrations

POLYP CORAL OLYP ORAL LYP RAL YP AL P L CORAL POLYPThere are many new Wolfram Demonstrations to peruse. The Houses and Utilities Crossing Problem, Half-Distance Rules with High Resolution, L'Hospital's Rule for 0/0 Forms, A Triangle Model of Criminality, Dice Probabilities, Spectral Realizations of Polyhedral Skeleta, Simulating Harmonographs, Passing a Cube through a Cube of the Same Size, and Reduce-Replicate-Rebuild are worth a look.

Rubik's Cube vs Octopus

Octopi like Rubik's cubes. Here's a story and picture.

Rubik's Cube vs Tiger

Tigers like Rubik's cubes. Here's a video. (I posted Spiderman vs Rubik's cube a few weeks ago).

Rubik's Cube vs Will it Blend?

"I'm going to press the solution button." (Thanks, Kara)

Forced Magic Square

It's easy to make a square with numbers 1-16 in order.

1	2	3	4
5	6	7	8
9	10	11	12
13	14	15	16

9	4

Add a second square, so that for any pair of numbers 1 to 16, the chosen pair will be in a row, column, or main diagonal in exactly one of the two squares. The first row starts 9, then 4. What is this square? Hint: it's a magic square. Send Answer.

Puzzle-Up Competition

Emrehan Halici has started a new series of puzzles at puzzleup.com.

Two Tiny Polyform puzzles.

Puzzles by George Sicherman and myself. 1. Arrange the 4 pentiamonds

to make 2 identical shapes. 2. Arrange the 4 tritans to make 2 identical shapes (in red, below, from the Tan Tricks set). Both solutions are unique. Send Answer. I'll also offer $25 for an unsolved problem: Arrange the 25 pentapents into 5 identical shapes, each with 5 pentapents. Could be impossible.

45th and 46th Mersenne Primes Found

Verification has started for two new Mersenne primes. Sketchy details are at mersenne.org. A forum discussion is at mersenneforum.org.

SIGGRAPH Winners

The animation Mauvais Role won the Jury award at SIGGRAPH. Two other winners are Our Wonderful Nature and Oktapodi.

Cast Vortex

I just got a copy of the beautiful Cast Vortex. I haven't solved it, and I can't fathom how it got designed.

Henri Cartan Dies at age 104

Henri Cartan passed away on August 13. Science News and the New York Times had articles about him. The American Mathematical Society interviewed Cartan in 1999.

Seeing in 4 Dimensions

A full movie series about the 4th dimension has been posted at dimensions-math.org. Julie Rehmeyer has the story about it, Seeing in 4 Dimensions.

Arctic Becomes an Island

For the first time in human history, the Arctic is now an island (New York Times). Noaa.gov has an animation.

Non-rigid Polyforms

Alexandre Owen Muniz: I have a new web page for non-rigid polyforms. Also, a new section for pentomino chains on my misc. polyomino exploration page.

X and Z Pentacubes

George Sicherman: This is the smallest solution I've found for the X and Z pentacubes. It has 20 tiles with 4-rotary symmetry. I've also posted some new Galvagni figures for pentacubes.

Topsy Turvy puzzle: M. Oskar van Deventer: Here is a YouTube video of the Topsy Turvy puzzle, which I just have successfully prototyped with the help of Peter Knoppers and George Miller. This puzzle is an implementation of the M12 puzzle, published in the July 2008 issue of Scientific American by Prof. Igor Kriz. The M12 group is a so-called "simple sporadic group" of permutations of twelve tokens. Prof. Kriz used the permutations "invert" and "merge" to construct the M12 group. My tokens are twelve disks, numbered 1-12. By cranking the handle either left or right, the tokens are entered into the mechanism that rearranges the tokens. Although the permutations "left" and "right" are slightly different from those used by Professor Kriz, they construct the same M12 permutation group. Or phrased differently, they make same fiendishly difficult puzzle.

New Wolfram.com Front Page: Hotly following our new Demonstrations page change (now with 3636 math demos), we now have a new look for our main wolfram.com page. I've got many more updates planned for the weekend. Click the link to see the spiffy new animation.

Rubik's Cube: 22 Moves Suffices: Tomas Rokicki: Twenty-Two Moves Suffice.

With a total of 1.28 million cosets solved, we have shown that every position of Rubik's cube can be solved in 22 or fewer face turns.

This required approximately 50 core-years of CPU time contributed by John Welborn and Sony Pictures Imageworks.

No distance 21 positions were found in this search, despite solving a total of more than twenty-five million billion cube positions.

There is a short article in New Scientist (August 9th edition) on this problem and this result.

The same techniques for the proof of twenty-five moves were used, just on many more computers.

I have found 310 cosets with an upper bound of 18, and about 82,000 with an upper bound of 19 (or less); all the rest have an upper bound of 20 or less.

My most profound thanks to John Welborn, Sony Pictures Imageworks, Herbert Kociemba, and Silviu Radu, and any others who have helped me over the past couple of years.

Square Hole Drill and Other Demos: A slew of new demos at Wolfram Demonstrations are worth a look, especially the Square Hole Drill by Stan Wagon. A few more new demos include Triangle Interior, Prufer Codes, Dissections by Izidor Hafner, Line Shadows In Every Direction, The Disappearing Square, Projections Of The 16 Cell, and Albrecht Durer's Pentagon.

Fractal Behavior in the Josephus Problem: Student Daisuke Minematsu and his classmates have noticed that the Josephus problem has fractal behavior.

Gauss Code Loops: Since I was 6 or so, I've doodled with closed, self-intersecting loops. Jaime Rangel-Mondragon wrote a simple demo called Self Intersections In A Polygon, and that reminded me of Gauss codes, which are useful for knots. You may remember them from Martin Gardner's New Mathematical Diversions, in the chapter Victor Eigen: Mathemagician. As an example, draw a simple closed loop that crosses itself 3 times, and put an arrow on it. Following the path, the loop will cross itself 6 times. Label the odd crossings (the 1st, 3rd, and 5th) with numbers 1, 2, and 3. The even crossings (2nd, 4th, 6th) will be a permutation. Your drawing will look like one of the following loops:
: Note that each of the order 3 permutations can be represented as a loop. I then wrote a demonstration for exploring Gauss code loops. Every closed loop corresponds with a permutation, but not vice-versa. For example, (34512) requires a sixth crossing due to nonplanarity. What rule describes the permutations which can't be drawn as loops? Turns out that By Laszló Lovasz And Morris L. Marx solved this problem (Bull of the AMS, Jan 1976, p. 121-122) with a brilliant short paper: A Forbidden Substructure Characterization Of Gauss Codes. Puzzle: find a simple closed loop with 9 crossings that becomes a simple quartic graph when crossings are changed to nodes.
New Yorker Article on Puzzles: The Eureka Hunt: The article The Eureka Hunt by Jonah Lehrer in the New Yorker discusses insight and puzzle solving.
Prime Sums Contest: Hugo Pfoertner: We are now running a new round of the Al Zimmermann's Programming Contests on "Prime Sums". Jean-Charles will "retire" as a contest organizer and programmer of the contest webpage after the current contest, which will run until 10 Nov 2008. After 3 contest days we already have 78 participants, and the usual suspects like the extraordinary Vadim Trofimov from St. Petersburg in Russia already have taken the lead.

Trofimov has already has won previous contests. One of the most fascinating contests producing incredible patterns was the snake folding contest running until end of 2006, with Vadim as winner. In the meantime a small group of German mathematicians has continued to search for improved folded snakes. Their work is documented in two webpages at enginemonitoring.net and rwro.de. Two examples are the colored zigzag snake and the colored mid-snake. There is also a link to special closed snakes, like the one below. [Ed- A previous Zimmermann contest winner, Tomas Rokicki, recently proved that any arbitrary Rubik's Cube position can be solved in 23 moves or less. He solved it with the help of the Spiderman 3 renderfarm.]

Oskar's Interlocking Spirals: Oskar van Deventer: My artical on Interlocking Spirals was published in Puzzlers' Tribute, A Feast for the Mind. Here is a gif animation illustrating the geometry of the spiraling Interlocking Spirals. Does there exist a useful application of this geometry, other than puzzles? [Ed: any ideas? Oskar can reached at planet.nl, by using his name m.o.vandeventer]

The Politics and Polls of 538 Delegates: Some of the sites I've found interesting for the statistical analysis of the upcoming US election are fivethirtyeight.com and pollster.com. There are dozens of sites you can check (Google "electoral map"), and the predictions are literally all over the map. A different map of recent interest: The Arctic Map.
Photos from the Bridges Conference: Some photos of the 2008 Bridges conference are at Flickr. Below is a 3D printing of George Hart's Toroidal Helical Sweep.

Computer Beats Go Pro: From Slashdot: Bob Hearn writes "I was in attendance at the US Go Congress match yesterday where history was made: the go program MoGo, running on an 800-core supercomputer, beat 8-dan professional go player Myungwan Kim in a 9-stone handicap game. Most in the audience were shocked at the computer's performance; it was naturally assumed that the computer would be slaughtered, as usual. Go is often seen as the last bastion of human superiority over computers in the domain of board games. But if Moore's law continues to hold up, today's result suggests that the days of human superiority may be numbered." [Ed - Bob Hearn is frequently mentioned here. Bob Hearn's website has many spectacular articles.]
Large Hadron Collider and Rap: Incredible pictures of the Large Hadron Collider are available at boston.com. The official LHC site seems tame by comparison. There is also the Large Hadron Rap, a music video which sums up many aspects of the project in five minutes.
Domino Logic: Another video, by Neil Fraser, shows domino logic gates.
Colorful Sea Slugs: Nudibranchs, or sea slugs, are some of the most beautifully colored creatures around.
Places to buy puzzles: The comprehensive online puzzle shops seem to be brilliantpuzzles.com, seriouspuzzles.com, and puzzlemaster.ca.
Whotsits: From James Dalgety (puzzlemuseum.com): Some Wotsits can be found at BBC News: Midweek Quiz: Inventions.
Upcoming Convention Appearances: In case you'd like to see me at a convention, I'll be going to two in the near future. On Sep 26-27, in Oxford OH, I'll be an invited speaker at the Recreational Mathematics conference. On October 23-25, in Champaign IL, I'll give a talk at the Mathematica Users Conference.
Oskar's 4 Bit Mazes: Todd Neller: Back in 2001, you mentioned M. Oskar van Deventer’s 4-bit maze at clickmaze.com. I especially liked the non-progressive 4-bit maze variation, and it struck me as an excellent beginner electronics project for my students. I was inspired write a simple generator for such mazes at cs.gettysburg.edu.

This applet’s mazes are generated by a simple stochastic local optimization that respects some graph constraints in making graph changes, while meeting other constraints through the iterative improvement process. What are the best sources for maze generation algorithms? I’m aware of Pullen’s online list of standard maze generation algorithms, but in the case of 4-bit mazes, one is seeking to generate random directed graphs with given edge constraints. Are you aware of resources along these lines relevant to directed graph maze generation? [Ed: Any ideas? At gettysburg.edu, Todd can be reached at tneller. Oskar van Deventer: "Wow, your implementation is fantastic! Well done!"]
Costas Arrays: In Rulers, Arrays, and Gracefulness article, I mention Costas Arrays. 2,4,8,5,10,9,7,3,6,1 is one such array. On each row of the difference table, values are distinct. The site costasarrays.org is now dedicated to these objects. No arrays are known for orders 32 and 33.

ABC Conjecture: A page by Bart de Smit devoted to the ABC Conjecture is also worth a look. One nice new triple found by Ismael Jiménez Calvo: 23⁸37⁴ + 2²⁸3⁷11⁴19³61·127·173² = 1817⁴43²4817².
Cold Boot Attacks: Dick Saunders Jr.: Here is a link including an interesting video of an Encryption Cold Boot Attack. [Ed - Fascinating]
Pentaking Oddities: George Sicherman: I finally found a bilateral oddity for the last pentaking! It has 109 tiles.
A Problem Solving Competition: From SlashDot: "Today, the CADE ATP System Competition will pit about 20 of the worlds most powerful mechanical mathematicians against each other — and for the first time they can win not only honour, but a monetary prize. The systems will reason against the clock on tasks ranging from undergraduate math problems and Cluedo-like puzzles to figuring out the possible responsibility for terrorist attacks from giant knowledge bases. If you think that is not impressive enough, they are doing it at a rate of 12 problems per hour, all day long. The competition starts at 10 a.m. in Sydney, Australia, which is midnight UTC. Live results will be available at the competition page. For added geek appeal, most of the contenders are available under open source licenses, so if you are weak in logic you can hack up your own brain extension and run it on an iPhone."

Lyons + Mankiewicz = Monica Lewinsky + Z: The replacements of Ebert & Roeper are Lyons & Mankiewicz, which has an interesting anagram. Starting with that, I wrote a Wolfram Blog item about anagrams and transposals.
Erich Friedman's House, Arrow, and Zigzag: Erich Friedman: Connect the houses in pairs so that only 2 different distances are formed. It's harder than it looks! answer. This is an example of a House puzzle. I've also added more new puzzles to Erich's Puzzle Palace. Namely, Binary Product, Arrow, Zigzag, and Lightbulb.

2D Mastermind: Chris Innanen: Last night I threw together a game idea I had and today was passing it out for playtesting to some of my friends through IMs. One of them suggested I contact you for your opinion. So here it is: Mastermind Squared. [Ed - interesting. In a 2D field, move colored squares around until the across and down clues are all perfect.]
Tilting Sliding Block Puzzles: Alex Polonsky: There is a new puzzle game at puzzle4u.com, a tilting puzzle game called Spin-In. It's like a mechanical puzzle, but there is no way to built this game in the reality.
Bob Henderson: I hope you can look at SLED Gravity Blocks, a collection of 40 new virtual slide puzzles at Nick Baxter's site. [Ed - two very nice sets of sliding block puzzles based on tilting.]
Polyhex Compatibility: George Sicherman: I've posted a page of Mixed-Order Polyhex Compatibilities. Comments are welcome.
Equivalent Perimeter and Area: Denis Borris: I found these 2 right triangles for which 3 Heronian triangles have same Perimeter and Area: 204 - 560 - 596 (right), 200 - 578 - 582, 260 - 476 - 624, 296 - 435 - 629 all with P = 1360 and A = 57120. Second: 528 - 630 - 822 (right), 462 - 738 - 780, 500 - 666 - 814, 549 - 606 - 825 all with P = 1980 and A = 166320 These are the 2 lowest primitives (unless I goofed and missed some).
Multimagic Squares: Christian Boyer has posted new updates to multimagie.com. Part of it is a Coxeter 1941 problem, of a magic square of triangular numbers.
Spore Prototypes: Derrick Schneider: I'm now a programmer at Maxis, the company making the videogame Spore, and I thought you might be intrigued by the Biome cellular automata program we released. We've been releasing dev prototypes for our users to play with. Here's the link: spore.com/comm/prototypes. [Ed - Interesting programs. For cellular automata exploration, I prefer Mathematica, Demonstrations, NKS, and Golly.]
50 Thousand Tornados: The Tornado History Project has lots of data, videos, photographs and maps of 50 thousand tornados. For example, Here are the locations of the 51 Fujita-5 tornados since 1950.

Irfanview 4.2: My favorite imageviewer, Irfanview, just got an upgrade. If any of my Adobe programs could launch instantly, I'd use them more, but most of the time I prefer the instant results of Irfanview.
Rotary: David J Bush: In Christian Freeling's chess variant "Rotary," the board is a 9×9 square grid. The kings are circular disks with pointers in four equally spaced directions, oriented in one of two ways: like an × or like a +. With just the two kings on the board, each move consists of either switching the orientation of your king from + to × or vice versa without moving it, or moving it one space in one if its indicated directions followed by optionally switching its orientation. You may not pass. The object is to deliver checkmate. Stalemate is impossible. Under what conditions in this two piece endgame is it possible to force checkmate, as opposed to a draw due to insufficient material? A discussion is at boardgamegeek.com.
Abundant numbers: An abundant number is one where the sum of divisors other than itself is greater than the number. The smallest pair is 5775, 5776. The smallest triplet is 171078830, 171078831, 171078832. Bruno Mishutka found that 141363708067871564084949719820472453374 is the start of a quadruplet, as noted at Can You Find.
28 cuboids: Can you put 28 3×4×5 cuboids into a size-12 box? There are 3 solutions. This problem by Don Knuth was originally solve by George Miller. The problem of 27 cuboids is in Winning Ways, p. 914. An example of 27 cuboids is shown at box packing.
Jean-Charles Meyrignac, Crossword Champion: Usually, Jean-Charles is often noted here for incredible programmatic results. But he's also now the fastest French crossword solver.

Spacetime Arcade: Spacetime 3 is math program for portable devices. The designer, Chris DeSalvo, has also put together the Spacetime Arcade, a collection of flash-puzzle games, all with attributions and permissions from the original designers.
RAFAEL + NADAL = TENNIS: Rodolfo Kurchan: I have made this (base 10) alphametic: RAFAEL + NADAL = TENNIS. The solution is unique.
KrazyDad Puzzles: The KrazyDad Puzzle blog has a huge number of puzzles. He's recently added Penrose Slitherlink and Altair Slitherlink.
Oskar Online: Oskar van Deventer has various puzzle games online. In Threesome (Java), three colored dots must work together to escape. He also sent a recommendation for Zeparate (shockwave), you must pull out the colors you own before your computer opponent.
Sudoku Variations: Nrich.maths.org has 42 sudoku variations at the moment.
Go Problems: The site goproblems.com has thousands of well-organized go problems, searchable in many varieties and skill levels, with a built in player.
2008 US Puzzle Championship: I missed the online 14 June US Puzzle Championship. The excellent set of 20 puzzles (password gc9yj2) is still available for your testing.
Repton: Luke Pebody: I, like you, love playing DROD. Have you ever played the "Repton" series of Games from Superior Interactive? I have been playing them (on and off) since I was about 6. They are well-designed level-based games like DROD. Unlike DROD the decisions take place in real time. It is fairly similar to the classic game "Boulder Dash", but more puzzle-based.
L and X Pentominos: George Sicherman: The attached compatibility figure for the L and X pentominoes has 44 tiles. This improves on the famous 80-tile solution of "Polyomino Number Theory."

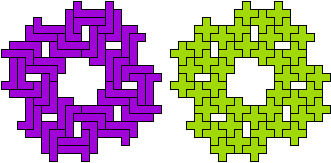
Commensurable Triangles: The paper Commensurable Triangles (pdf) by Richard Parris studies the problem of a triangle where one angle is a multiple of another.
Steve Sigur Passes: Steve Sigur, the author of the pending Triangle Book with John Conway, has passed on. The sites legacy.com, huffingtonpost.com, edublogs.org, and ajc.com have articles about him. His webpage on triangle geometry has many of his beautiful findings. With help from Colm Mulcahy, he delivered a final version of his book to publisher A K Peters shortly before passing.

Valentine's Day Maze on Games Magazine cover: The cover of the latest Games uses Robert Abbott's excellent Valentine's Day maze. You can also take a look at the latest version of his Theseus and the Minotaur.
25 Primes in Arithmetic Progression: Raanan Chermoni & Jaroslaw Wroblewski: 6171054912832631 + 366384×23#*n, for n=0 to 24. New longest known arithmetic progression of primes! (May 17 2008). [Ed - A paper with Wroblewski's method is available.]
Length 17 Cunningham Chain: Jaroslaw Wroblewski found x₁=2759832934171386593519, the start of a length 17 Cunningham chain. With x_n₊₁ = 2x_n+1, the x_n are prime numbers up to x₁₇. He found a total of four record setting length-17 Cunningham Chains.
Plouffe Invertor: Simon Plouffe posted a message about 2.5 billion mathematical constants at sci.math.symbolic.
Watering a Magic Square: Craig Knecht has put together a page about water retention in topographical magic squares. His other magic square models are also very clever.
23 Moves is Enough: Tomas Rokicki has proven that any arbitrary Rubik's Cube position can be solved in 23 moves or less. It was solved on the Spiderman 3 renderfarm at Imageworks.
4D Megaminx Puzzle: Roice Nelson: I recently published a 120 cell permutation puzzle (which could be considered the 4D analogue of Megaminx), and I wanted to let you know in case you'd like to share it with the mathpuzzle.com readers. [Ed - Just in case Rubik's cube is now too simple.]
The Digit Puzzle: Alex Polonsky: I think you would be interested in my new puzzle-game called Digit. It can be found at www.puzzle-4u.com. All levels of this puzzle-game were created by computer program. [Ed - An incredible series of puzzle miniatures. For each move, you may pick up and move a single piece. To win, the treasure chest must be visible with all pieces placed.]

Bozzball's Puzzling World: Luke Pebody: I have released over 600 logic puzzles at bozzball.blogspot.com, with more appearing daily. [Ed - A large variety of logic puzzles is there.]
PennyDell Puzzles Site: Another site with daily puzzles: pennydellpuzzles.com. A new site from the largest publisher of puzzle magazines.
Conceptis Relaunch: Conceptis Puzzles also has daily logic puzzles, and just got relaunched.
Puzzle Picnic: For even more puzzles, Puzzle Picnic has 600 logic puzzles and counting.
Power Problem: Erich Friedman: everyone knows that 2⁴ = 4². But hardly anyone knows 2⁵ + 2⁷ + 2⁹ + 5³ + 5⁴ = 5² + 7² + 9² + 3⁵ + 4⁵. Are there examples of this type with fewer terms? (Also see his recent wonderful Math Magic findings, including Frame Tilings, Powers (183425228501 + 438841438125 = 622266666626, 183425228501² + 438841438125² = 226226622266262266222626), Polyforms in Parts, and Square Packing. Also take a look at his lovely powerpoint presentation Rep-tiles.)
Journal of Number Theory on Youtube: The Journal of Number Theory is now on YouTube.
Simple Groups at Play: At the Scientific American site, some java puzzles based on Mathieu groups have been made available. Ridiculously hard, but worth a look.
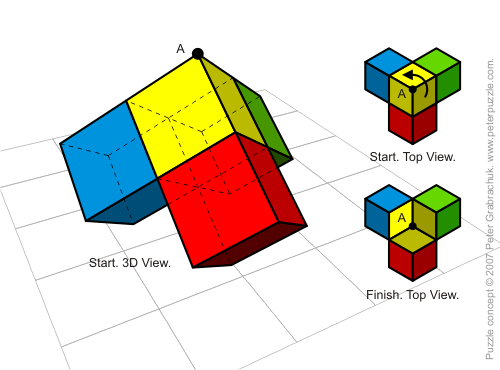
Four Cubes Puzzle: Peter Grabarchuk (peterpuzzle.com): You have four identical color cubes (1x1x1) which form a shape shown in the illustration; yellow cube lies on the other three. The object is to determine the distance which corner A of the yellow cube passes when the cube rotates counter-clockwise for 60 degrees from Start to Finish (see both Top Views). Note that while rotating, the yellow cube remains in the continuous contact with the other three ones which do not move. (solution) [ See also his Simple Book of Not-So-Simple Puzzles.]

Total Gadha: Sanjeev Singh: I am a math teacher from India who runs his own Math and English website titled totalgadha.com. I write math chapters for students preparing for competitive MBA exams. If you think they are useful, can you mention our website on your blog? [Very nice, so yes.]
Gardner Article: John Gowland: Saw this article in London (formerly Manchester) Guardian Weekend supplement. It talks about Gathering for Gardner, and gives a puzzle by your friend Wei-Hwa Huang. I was one of those in late 50s who discovered that it was OK to enjoy math! I don't seem to find time to make any crossnumbers since I retired (never been so busy), but I enjoy teaching extra High School Grade 11 and 12 math twice a week.
Slanty Sliding Block Puzzles: Relatively new at puzzlebeast.com are Slanty Sliding Block Puzzles.
Povray Short Code Contest: The results of the Povray Short Code contest are stunning.
Computational Geometry: The Computational Geometry Algorithms Library is a great resource for code and explanations involving this topic.
Lightning in a Block: Theo Gray explains Lichtenberg figures -- lightning trapped in plastic. Another neat popsci link is self-repairing rubber.
Cabtaxi(10) = 933528127886302221000: Christian Boyer: After his recent work on Taxicab(6) confirming the number found as an upper bound by Randall Rathbun in 2002, Uwe Hollerbach (USA) confirmed this week that my upper bound constructed in Dec 2006 is really Cabtaxi(10). See his announcement.
933528127886302221000
    = 8387730³ + 7002840³  (1) = 8444345³ + 6920095³  (2)
    = 9773330³ - 84560³  (3) = 9781317³ - 1318317³  (4)
    = 9877140³ - 3109470³  (5) = 10060050³ - 4389840³  (6)
    = 10852660³ - 7011550³  (7) = 18421650³ - 17454840³  (8)
    = 41337660³ - 41154750³  (9) = 77480130³ - 77428260³  (10)
See also http://cboyer.club.fr/Taxicab.htm, with updated tables of Taxicab and Cabtaxi numbers. You can also freely access to my paper published in Journal of Integer Sequences, with explanations on how this number was constructed, before to be proved the real Cabtaxi(10) number. Reminder:
-Taxicab(n) is the smallest number expressible as a sum of two cubes in n different ways.
-Cabtaxi(n) is the smallest number expressible as a sum or difference of two cubes in n different ways.
Ammann Chair: The Ammann Chair is one of many demonstrations recently added at the Wolfram Demonstrations site. Other recent additions include Conformal Mapping, Irregular Tilings, Intrinsically Knotted Graphs, Fifteen Great Circles, Game of Hecks, and the Four Runner Problem.

Morpion Solitaire Site: Christian Boyer: First update of morpionsolitaire.com: thanks to Michael Quist, the 4T and 4D games are now solved! But 5T and 5D still open... Who will improve the current records? An easy game, only paper and pencil needed: 5T Morpion Solitaire (the original version of Morpion Solitaire) is one of the rare games still having its best scores produced by hand... and more than 30 years ago! Computers greatly helped on 4T/4D/5D, but seem fully unable on 5T.
Fibonacci Seed Hearts: Some gorgeous pictures of Fibonacci Numbers and Nature are available at a page maintained by Ron Knott.
Eric Harshbarger's 7th Puzzle Party: Eric Harshbarger: Thought you might like to read the write-up I've done about my latest puzzle party, which took place the week after the Gathering for Gardner.
Polyhedra Stellations and Sculptures: I first mentioned Vladimir Bulatov 7 years ago. I'd mentioned his gorgeous stellations applet. He is now offering beautiful metal polyhedra sculptures.

CalcZilla: A bloody cartoon about integration: Calczilla.
Crossword Compiler: One puzzle program I use a lot is Crossword Compiler 8.1. If you'd like computer assistance for constructing a crossword puzzle, this is the program to get.

PayPal
$10	Hoffman-Singleton
$20	Chaos Tiles
Buy books

Content on this page requires a newer version of Adobe Flash Player.

Content on this page requires a newer version of Adobe Flash Player.