MathPuzzle.com

Mathematica Turns Twenty: Mathematica Turns 20, Differential Geometry Carved in Stone, and NUMB3RS Season 4 Wrap are all recent entries at the Wolfram Blog.
Riddles of the Sphinx: The Riddles of the Sphinx by David Bodycombe is a superior puzzle book, with over a thousand good puzzles.
Simple Book of Not-So-Simple Puzzles: The Grabarchuk family has published the Simple Book of Not-So-Simple Puzzles through A K Peters. More than a hundred puzzles you haven't seen before.
Jeux Math: Christian Boyer: "Jeux Math" = "Math Games" You should appreciate this issue! Hoping you read French at least a little. [ CB very kindly sent me the supplement to the French version of Scientific American. It's available for purchase for 7 euros. 120 glossy pages jam-packed with about a thousand great color recreation mathematics figures. No ads. All text is in French. 31 excellent articles.]
Cubic Dissection: Eric Fuller: Various new puzzles can be seen in in the Cubic Dissection Catalog, and in the Cubic Dissection Marketplace.
No-4-in-a-plane: From a 3x3x3 grid, pick 8 points so that no four are in a plane. Ignoring rotations and reflections, the answer is unique. Addendum from Edwin Clark: There is a beautiful proof that 9 points isn't possible, by Achim Flammenkamp. Addendum from Jonathan Welton: No 4 in a plane: I remember this being posted to rec.puzzles by Torsten Sillke in 1992. Took a while to find the answer, which I recall having a 3-way rotational symmetry, and looks a bit like a propeller. Addendum from Ed Pegg Jr: I put together a demo to show 211 order-4 solutions.

The Long Awaited DROD Trailer: DROD (Deadly Rooms of Death) is incredible. I highly recommend starting with Journey to Rooted Hold, my favorite puzzle game ever. From there, take on The City Beneath, the best game sequel ever made. And now, there is a trailer for the game. Definitely worth a look at Youtube.
No Four in a Row: George Sicherman: I presume that Haugland's comment that the size of those polyominoes is limited is based on the obvious (if you don't get confused by all the variables) extension of Van der Waerden's Theorem to two dimensions. Anyway, that suggests a much easier puzzle.

Adjoin three different pentominoes to make a polyomino with no four cells collinear. (answer)

I've put up some more pages of Baiocchi figures-- for polyhepts, polyocts, and polyenns. You may have seen the polyhepts and polyocts at Erich's website. The polyenn figures are new.
Short Chess Games: Each of the following is a uniquely determinable game of chess (answers):
4... Qb5#
5.Ng3#
5.Qxe4#
5... Rh1#
6.Nd3#
6.gxf8=N#
Rounder Router: A lot of applets for exploring the Rounder Router are available at Steve Witham's page.
Visualization of Seifert Surfaces: A neat program for looking at Seifert surfaces is Seifert View.

Solar Ovens: The miracle of parabolic reflection has been in the news lately. In Darfur refugee camps, fuel oil and firewood are both difficult to get, so solar cookers by the name of CooKit are being distributed. I also liked the DSPC plan, and the Windshield Shade Solar Cooker. The last one adds a few pieces of velcro to a normal cheap carshade. I plan to prepare some steelcut oats with mine -- I've always felt slightly guilty and inconvenienced by the one hour cooking time.
Voronoi Diagram Video by Theo Gray: Theo has posted a video about Voronoi Diagrams to youtube. This is linked in with the Demonstrations project.
Maxton's Metal Puzzles: Maxton's Metal Puzzle Gallery is getting to be fairly impressive. "Well this is different. I milled this Micro-Conundrum out of something called M3 metal; M3 is short for MacroMolecular Metal. It's a new composite material."


Amy Young, for Numb3rs: Amy Young is one of my colleagues on the Numb3rs team, and was recently featured on Inside Illinois. We recently gave a pre-awards talk to a thousand contestants of the ICTM. Incidently, season 4 of Numb3rs wraps filming this week, with 18 episodes.
Wolfram Research Blogs: A whole series of great blogposts have been made at the Wolfram Research Blog. Three blogs in particular: Two Hundred Thousand New Formulas, Making Photomosaics, and Bernoulli Record.
Hilbert's 10th problem & Julia Robinson: An online film about Julia Robinson is available. Some news about the film is available.

Karl Scherer Puzzles: Karl Scherer has made a great series of puzzles for the Demonstrations project. A really great series -- with more than 20 variations for each puzzle type.

Optimal Polyform Division: Erich Friedman's Math Magic last month dealt with optimized polyform divisions. For example, what is the large set of 2 identical pieces that can be cut from a p-pentomino? The below division attains .928+ of the figure and was found by Dick Hess. Many more best known solutions are presented by Erich. May's Math Magic also deals with optimized dissections.

Chess Puzzles by Leonardo da Vinci: Leonardo da Vinci may have illustrated a treatise on chess puzzles. If verified, this would likely become the world's most valuable puzzle book.
Sebastien Perez-Duarte Art: The work of Seb Przd on Flicker explores the world of conformal mappings. I especially like his piece "I'm telling you, it's not straight!"



Weird Polyomino: Erich Friedman: I found this on the EIS: a 142-omino found by J.K. Haugland with the property that no 4 square centers are equally spaced on a line. Is this the largest one? Addendum by Jan Kristian Haugland: I noticed accidentally that you guys were discussing my 142omino with no four in a row on mathpuzzle.com. I would like to comment that I proved that the size is bounded by generating all possible paths. I believe that 142 is optimal, although I don't have a proof. It is possible to rearrange a few of the squares to create a handful of other 142ominoes with the same property (but I forget which ones).

Walter Trump's Order-4 Magic Cube: Some old news, but news to me, Walter Trump has made an improved order-4 magic cube. Fermat, in 1640, made the first magic cube, with 64 magic lines out of 76. Trump's cube, found in 2004, has 72 magic lines. Richard Schroeppel proved 76 magic lines was impossible in 1972.
New Burr Tools: Rhombic Dodecahedra can now be modeled with Burrtools, with a major new release (free).
Shortest Chinese Checkers: George Bell has found the shortest game of Chinese Checkers.
Defendius Door Chain: Joshua Martell: Hi Ed. This looks like something you might find amusing. A normal door chain based on a maze. Jeffrey Smith: The Defendius door lock was on Thinkgeek.com as one of their April Fool’s products.
Hula Hoop Dome: A giant dome made with hula hoops has been made.
Non-crossing Knight's Tour in 3-Dimension: Awani Kumar: Non-crossing knight's tours in 3-dimension is a new field of research. The author has shown its possibility in small cuboids and in cubes up to 8x8x8 size. It can also be extended to larger size cubes and cuboids. The author has achieved jumps of length 15, 46, 88, 159, 258 and 395 in cubes of size 3x3x3, 4x4x4, 5x5x5, 6x6x6, 7x7x7 and 8x8x8 respectively. This amounts to covering 59%, 73%, 71%, 74%, 76% and 77% cells in these cubes.
Ghost/Vampire/Zombie Mirror Puzzles: Otto Janko: I wrote an applet for Ghost/Vampire/Zombie mirror puzzles: You can also find it on David's website, The Griddle.

307,409 Math Formulae: The Functions site, functions.wolfram.com, has undergone a very major update. It now has 307,409 math formulae, all multiply verified.
Rubik's Cube -- 25 Moves or Less: Tomas Rokicki (arxiv.org/abs/0803.3435): How many moves does it take to solve Rubik's Cube? Positions are known that require 20 moves, and it has already been shown that there are no positions that require 27 or more moves; this is a surprisingly large gap. This paper describes a program that is able to find solutions of length 20 or less at a rate of more than 16 million positions a second. We use this program, along with some new ideas and incremental improvements in other techniques, to show that there is no position that requires 26 moves.
The Tesla Roadster: For my next car, I'd like to get a Tesla Roadster, a plug-in electric vehicle. The 2008 models are sold out, and I don't have the money for the 2009, but I can definitely have it on my wish list. Jay Leno just got the first production model, and he made a Tesla video blog about it. I learned about it after watching the incredible documentary, Who Killed the Electric Car. One of the chief murderers was the California Air Resources Board (CARB), which gutted most of the goals for zero-emission vehicles after an oil company stooge, Alan Lloyd, gained control of the board. Most electric cars were then taken back by the automakers and sent to crushers. Now that Tesla Motors is rolling cars off the production line, the CARB is taking a new tactic to penalize Telsa Motors for making clean cars. The CARB public hearing will be March 27th (tomorrow).

160 Square Mile Ice Shelf Disintigrates: Down in Antartica, a massive part of the Wilkins Ice Shelf has collapsed.
Spidronized Archimedean Solids: Hmmm... spidronized solid description, or just a site link and picture? I'll go for the picture, which is a small piece of a huge, beautiful site by Dániel Erdély.

Numb3rs Promo spoofs Mac/PC Ad: Numb3rs returns next week, with some (spoiler) Voronoi diagrams (end spoiler). Morrow and Krumholtz have spoofed the Mac/PC ads to make a very cute Numb3rs promo.

Fugue for Friday: I like the Music Animation Machine -- very visually intuitive method for signifying music, for a nonmusician like me. Also used by Peter Schickele.

Chess Puzzles by Leonardo da Vinci: Leonardo da Vinci may have illustrated a treatise on chess puzzles. If verified, this would likely become the world's most valuable puzzle book.
Polyform Curiousities: Colonel George Sicherman, with help from Mike Reid, Claudio Baiocchi and Károly Hajba, has recently added hundreds of new discoveries to his Polyform Curiousities pages.
Number curiousity: Erich Friedman: A = 912 and B = 2091 have an interesting property: They are not palindromes or reverses of each other, and yet A + B = 3003, A^2 + B^2 = 5204025, and A^3 + B^3 = 9900990099 are all palindromes. Likewise, C = 82741 and D = 144486 have a different interesting property: They do not contain any 0's, and yet C + D = 227227 and C^2 + D^2 = 27722277277 both use the same two digits. These are the largest pairs I know of with these properties. (Related Math Magic page)
Tightly Packed Squares: David Cantrell: I see that you mention Tightly Packed Squares at the beginning of your update. If you like that sort of thing, see the Math Magic packings, esp. the last one.
Faking Gold Bars: The Bank of Ethopia recently accepted fake gold bars, made out of steel. Also, gold has gone to over $1000 an ounce. Theo Gray put together a nice blog entry about fake gold. You can see more of Theo's columns here.

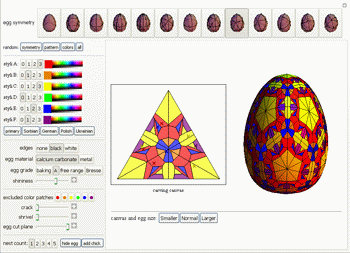
Eggs Demonstrations: Just in time for Easter, a variety of egg-coloring demonstrations have been made.

Dissection Demonstrations: Izador Hafner has made a few dozen dissection demonstrations, based on the work of Greg Frederickson.

Pi Day blog: I wrote up a few details about Pi day in a Pi Day Blog.
Interesting papers on Arxiv.org: The Inverse Simpson Paradox (How To Win Without Overtly Cheating)
Authors: Ora E. Percus, Jerome K. Percus
Given two sets of data which lead to a similar statistical conclusion, the Simpson Paradox describes the tactic of combining these two sets and achieving the opposite conclusion. Depending upon the given data, this may or may not succeed. Inverse Simpson is a method of decomposing a given set of comparison data into two disjoint sets and achieving the opposite conclusion for each one.
Sheep Collisions: the Good, the Bad, and the TBI
Michael Courtney and Amy Courtney
The title page of Chapter 9 in Fundamentals of Physics shows a dramatic photograph of two Big Horn sheep butting heads and promises to explain how sheep survive such violent clashes without serious injury. However, the answer presented in sample problem 9-4 (p. 213) errs in presuming an interaction time of 0.27s which results in an unrealistically long stopping distance of 0.62m. Furthermore, the assertion that the horns provide necessary cushioning of the blow is inconsistent with the absence of concussions in domestic breeds of hornless sheep.
The Free Will Theorem and Thou Shalt Not Clone One Bit!
Authors: John Conway, Simon Kochen
Abstract: On the basis of three physical axioms, we prove that if the choice of a particular type of spin 1 experiment is not a function of the information accessible to the experimenters, then its outcome is equally not a function of the information accessible to the particles.
Introduction to the Prisoners Versus Guards Game
Authors: Timothy Howard, Eugen J. Ionascu, David Woolbright
We introduce a two-player game in which one and his/her opponent attempt to pack as many prisoners as possible on the squares of an n-by-n checkerboard; each prisoner has to be protected by at least as many guards as the number of the other prisoners adjacent.
Sustainability: A Tedious Path to Galactic Colonization
Authors: Y. Dutil, S. Dumas
Civilization cannot sustain an exponential growth for long time even when neglecting numerous laws of physics! In this paper, we examine what are fundamental obstacles to long term survival of a civilization and its possibility to colonize the Galaxy.
Drip Paintings and Fractal Analysis
Authors: Katherine Jones-Smith, Harsh Mathur, Lawrence M. Krauss
It has been claimed that fractal analysis can be applied to unambiguously characterize works of art such as the drip paintings of Jackson Pollock. This academic issue has become of more general interest following the recent discovery of a cache of disputed Pollock paintings. We definitively demonstrate here, by analyzing paintings by Pollock and others, that fractal criteria provide no information about artistic authenticity.
Michael Trott's Version of an Egg: Michael Trott pointed me to all the Arxiv links above, and runs the amazing site mathematicaguidebooks.org. He's made available a demonstration there (usable with Mathematica Player) that explores dozens of egg symmetries.

David Gale Passes: Math Recreationalist David Gale died on March 7, at age 86. He solved the n-dimensional Ramsey problem, invented Chomp, won the John von Neumann Theory Prize, wrote material for MathSite, wrote the book Tracking the Automatic Ant, and ran the Mathematical Entertainments column in Mathematical Intelligencer. He will be missed.
Arthur C. Clarke Passes: He was one of the leading voices for promoting mathematics and science, and a great influence on my life. We corresponded several times.

Tightly Packed Squares and other Demonstrations: Many more demonstrations have been added to the Wolfram Demonstrations Project, including Color Blindness, Tightly Packed Squares, The Cake Icing Puzzle, Sicherman Dice, Trajectories of the Logistic Map, 2-pire Map, Fractal Right Triangles, and the Three Distance Theorem. If you'd like to try your hand at making a demonstration, and don't have Mathematica 6, feel free to send me a proposal. Over 2500 free mathematical demonstrations, and growing.

James Randi's The Amazing Show: Podcasts from the world's leading skeptic, James Randi, are available at his site for The Amazing Show.
Werner Icking Music Archives: I was pleasantly surprised when I found a huge collection of free public domain midi and music files at icking-music-archive.org.
Sound illusions: Some nice auditory illusions are available at Five great Auditory Illusions (New Scientist), and at Research and Musical Demonstrations.
Credit Card Forensics: The mathematics of credit card crime is wonderfully explained in an article by Hal Berghel.
Ebb and Flow of Movies: The New York Times has a great graphic based on movie box office receipts: The Ebb and Flow of Movies.
Numb3rs at the Emmys: The write-up of Numb3rs at emmys.tv is now up. I never imagined I'd get mentioned there.
A Chess Problem Tournament: Itamar Faybish: I am preparing a new chess series competition to start in 2 weeks, if you are interested. It will not be a series helpstalemate as before, but in the same spirit. Hopefully as fun as the previous ones. I cannot yet reveal the exact nature of the competition, which will be presented only on the 7th of March.
Counterexample to Fermat's Last Theorem: 70^3 = 3 4 3 0 0 0
212^3 = 9 5 2 8 1 2 8
-----------------------------
462^3 = 9 8 6 11 1 2 8

found by Erich Friedman. The latest Math Magic also deals with sums of powers.
A Benedictine Monk Polyformist: Eswaran Narasimhan: Please see the page of Father Magnus Wenninger OSB. Beautiful polyhedra creations, colourful, and with a guide. Father Magnus' creations are interesting!! [Very nice. And some are for sale.]
Magic Square Wheel Methods: Eddie Gutierrez has written up some Magic Square methods at oddwheel.com.
Mathematical Art: Slashdot wrote up a Science News article about Mathematical art.
Mathematica User Stories: Wolfram Research now has a Youtube page: Portraits of Success with Mathematica.
Phun Marble Machine: Phun is an excellent free physics engine, similar to the Crayon Physics engine, but more powerful. Livio Zucca made this Marble Machine with it. Xerol Oplan pointed me to this Marble Clock.

A Circle Packing Puzzle: Bill Gosper: For the last several years I've sought to make challenging puzzles based on packing a given set of disks into a given cavity. Unique solutions are nicer and presumably harder to find, so no two disks want to be close in size. On the other hand, if the sizes are widely disparate, the smallest disks fit between the largest, and are simply redundant. These conflicting criteria become nearly impossible to meet as the number of disks reaches twelve, where the sheer number of configurations also works against uniqueness. To make matters worse, it appears to be infeasible to check for uniqueness computationally, or even solve these puzzles at all without simplifying assumptions.
: For circular cavities, the best I have done is eleven disks (The Huddle), with various attempts at twelve (Twubblesome Twelve, TTII, ...) cooked by expert solvers. Perversely, the unintended solutions have generally been *looser* than the apparently close-packed "mathematical" solutions, which probably *could* be found by a sufficiently clever program.

Noncircular cavities enormously complicate things for both the designer and the solver. E.g., the designer no longer has a family of cavity-preserving Moebius transformations on the disk sizes, and the solver (e.g., a program) is faced with a continuum of distinguishable places to start. And by precluding rotations and reflections, an asymmetrical cavity cuts the solution space by another factor of 4. Perhaps best of all, given the size constraints on the disks, it seems possible to fill a slightly greater percentage of a noncircular cavity, although the computations are formidable. Greater coverage leaves fewer solutions.

Experts again cooked my early attempts (Octave, Arnold Laidanegger, ...) but for Arnold Dozenegger, I spent months repeatedly solving systems of 33 polynomials, many with 3367 terms, and 36 unknowns. It very probably falls short of optimal coverage, but so far, no one has found even the intended solution, let alone a bogosity.

[Ed - In addition to the demo above, a picture is at gosper.org. If you are intrigued enough to get a copy of the latest version after years of analysis, even after hearing the price is $300, Bill can be contacted through yahoo.com with username rwmgosper.]
Anagram: Every few months, someone forwards me a letter about anagrams. A comprehensive list of anagrams that have been published in The Enigma is at puzzlers.org.
Animator vs Animation: Two works by Alan Becker, Animator vs Animation and its sequel, make good fun of Flash and the Windows Desktop.
Sperner's Triangle Game: Play one of three colors. Don't make a small triangle with all three colors. You can play The Sperner Game online. Then you can read the Sperner Game paper to see how difficult it is.
Baiocchi Figures: What is the most symmetrical figure you can make with 12 T pentominoes? Colonel Sicherman records everything up to heptominoes in his new Baiocchi Figures page, named after Claudio Baiocchi.

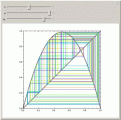
The Random Chord Paradox: I added the Random Chord Paradox to the Wolfram Demonstrations Project. What are the odds a random chord measures more than 1.732, the square root of three (and Washington's birthyear)? If the height is chosen randomly, 1/2. If two points on the rim are chosen randomly, 1/3. If a random point inside is used as the midpoint, 1/4. A new method of randomness occurred to me. Two random points inside the unit circle define a chord. What are the odds that this chord is longer than the square root of three? Send Answer. I made a blog post about Demonstration Puzzles for Puzzle Day.

MIT Puzzle Hunt: Steve Nadis wrote up the MIT Mystery Hunt. The Little Black Book Puzzles from the hunt are now online.
Sliced Menger Cube: What does a sliced Menger Cube look like? Answer.
The Darkest Material: BBC writes up an array of carbon nanotubes that makes the darkest material ever made, developed by a team led by Pulickel Ajayan.
Abe Lincoln Must Die: Cartoon duo Sam and Max have done the impossible: episodic computer games, delivered on time. In addition to their unique humor, the series has a number of good puzzles. One of their episodes from last season, Abe Lincoln Must Die, is now available for free.
Self-Affine Tilings: Kenyan and Solomyak have written an interesting paper on self-affine tilings. Another semirecent paper is George Bell's Diamond Solitaire.
Happy 70th Birthday, Donald Knuth: Jeffrey Shallit's Recursion blog celebrates Knuth's 70th birthday.
Benoit Mandelbrot Judges Fractal Art: The Fractal Art Contest 2007 had many stunning images, and was judged by Benoit Mandelbrot. Enjoy the pictures.
Bell Kites: Alexander Graham Bell, in addition to inventing the telephone, was a constructor of octahedral truss kites. Some kite-builders have built some huge examples, as seen on the site.
What song is this?: A very impressive youtube song. Lots of cute effects, with no tricks but memorization.
Spinning Girl Illusion: Wei-Hwa Huang hacks the Spinning Girl Illusion.

Theseus and the Minotaur: Robert Abbott: I finally got Theseus and the Minotaur published as a pretty interesting download. The publisher is Kristanix Games, a company run by a couple of bright Norwegians. Toby Nelson and I will actually get royalties (5%) for the game. I really hope this new version gets popular. I have a write-up about it on my home page. We only have 85 levels, but I'm working on more -- they are all good.
Crayon Physics: I like the game Crayon Physics a lot. A deluxe verse is rumored to be coming out soon.
Luke Pebody Puzzle Blog: Luke Pebody: I have started a puzzle blog at bozzball.blogspot.com. Currently there are only 2 sudoku's and 1 "sudoku X" but more puzzle types will be coming over the upcoming weeks, including: * British-style Cryptic Crosswords * Battleships * Kakuro and more...
A blank and a blank: Rearrange the letters of ABROGATION to get an ending for a sentence that starts "A blank and a blank ...." You'll need to fill in the blanks yourself.
Cubic Dissections Puzzle Marketplace: cubicdissections.com now has a marketplace for high-quality, craftman-made puzzles. Also some one-of-a-kind pieces, antique puzzles, and experiments.
Point Flexagons: Scott Sherman: I noticed that a couple years ago you posted the discovery of the dodecaflexagon, a flexagon-variant with 12 triangles per face. This joins the flexagons Martin Gardner originally described - the hexaflexagon (6 triangles per face) and tetraflexagon (4 or 6 squares per face) - plus the various flexagons made from other polygons (pentagons, hexagons, etc.). More recently, I’ve generalized this to point flexagons (point hinges instead of edges) and triangle flexagons made from any number of triangles per face (e.g. 5 isosceles triangles per face or 4, 6, 8, 10 or more right triangles per face). I’ve also created a number of puzzles on some of these triangle flexagons. My main page for these flexagons is http://loki3.com/flex/index.html. Enjoy!
2008 puzzles: Erich Friedman: Using each of the following collections of digits, along with the usual arithmetic signs ( + - x / ^ ), make a total of 2008. {1,3,8,8,8} {1,4,4,4,8} {2,3,8,8,8} {2,5,9,9,9} {2,7,8,8,8} {2,8,8,8,9} {3,4,8,8,8} {4,4,4,8,9} {4,5,8,8,8} {5,6,6,6,8}.
SSAN puzzle: Bernardo Recaman: I had great difficulty trying to remember my social security identity number, a long string of digits, until I realized that it is the largest number in which every block of two adjacent digits is a different prime or square number. What number is it?
The Complete Set of Oddities: Col. George Sicherman: Mike Reid and I have finally completed the catalogue of heptomino oddities. Every one of the 108 heptominoes has an oddity!

Demonstrations: Quite a few of the most recent Wolfram Demonstrations have been mine. I've been authorized to make an offer to the mathematical hobbyists and diagrammers out there. Mail me a proposal for something that hasn't been made as a mathematical demo, and include a short write up of your math hobbies. The best proposals will get a temporary Mathematica 6 license. As of today, over 2300 math demonstrations are online, and I'm hoping to break 3000 before the end of the year.

Math Factor: The latest Math Factor podcast is an interview with me. Through the miracle of post-editting, I sound amazingly good and smart. Search for Math Factor in iTunes to find it.
Nanomechatronics: Add a single letter to "nanomechatronics" and rearrange to get the full name and title of somebody currently in the news. ANSWER: nanomechatronics + J = Senator John McCain.
The Gewirtz and 77 Graphs: My contest from last month has been claimed by Jonathan Cross and Tony Forbes, who each used some ingenious methods to crack the 77 graph and the Gewirtz graph.
TeX the World: TeX the World is a Firefox plugin usable with greasemonkey. It converts TeX formulas in [;;] to nice formulas, for example [;$e^{i\pi}+1$;], [;${-b \pm \sqrt{b^2-4ac} \over 2a}$;].
Approximation Puzzles: Erich Friedman: Using only + - x / ( ) and decimal points,
1) approximate pi to three significant figures with three 2's.
2) approximate e to four significant figures with four 7's.
3) approximate the euler gamma constant to four significant figures with four 8's.
45 Thousand Ballpoint Balls: Bathsheba Grossman: Hi, I thought you might like this (14 Meg): (main link, mirror 1). It's a lot of ball-point pen balls suspended between two glass plates, being vibrated by a small motor. It does these interesting things: crystal-like interface boundaries and fracture lines obviously, but also cellular automata-like features such as little triangular configurations that seem to propagate like Life gliders. This device belongs to Ward Fleming (pinscreens.net, he invented those pin screens that one makes faceprints on), and I couldn't help thinking it'd make a nice interactive installation somewhere.
The Hexacubes: Kadon Enterprises has put together a hexacube set for a collector.

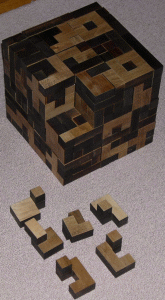
The Griddle: David Millar has been managing to make a lot of puzzle updates at The Griddle. I like his series of Ghost/Vampire/Zombie mirror puzzles.

PayPal
$10	Hoffman-Singleton
$20	Chaos Tiles
Buy books