Material added 13 April 2004
At gamepuzzles.com, a new issue of The Life of Games is available. Erich Friedman's Strobogrammatic Expressions at Math Magic this month is quite interesting. At Fools Errand, you can see Cliff Johnson's April Fool's hunt. Cihan Altay will launch the PQRST 09
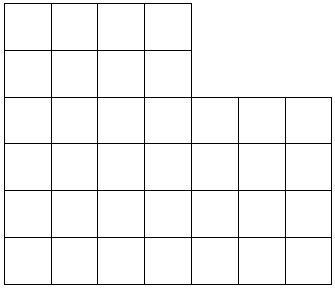
solving competition on 17 April 2004. The below is one of Cihan's
puzzles. Divide the object into 2 identical shapes, or 3
identical shapes, or 4 identical shapes.
The 123456 folding puzzle is very nice. Put it on cardboard, and have fun showing it to your friends. Craig Kaplan's work on geometric ornamental tiling is fascinating.
I recently had the pleasure to try out the Quantian distribution.
This is a math-intensive Linux distribution that runs directly off of a
CD. For any computer, you can put in the CD, reboot, and you'll
be running Quantian Linux in a few minutes (keyboard, mouse, and all
else are auto-detected). When done, reboot, remove the CD, and
you are back to your current system. Your hard drive will be
untouched. It has many math packages I've wanted to try for
awhile. Several of them, such as LyX and TeXmacs, have nontrivial set-up procedures. I was delighted to be able to try them all. GAP, Gnu Scientific Library, Python modules including Scientific and Numeric Python, apcalc, aplus, aribas, autoclass, DrGeo, euler, evolver, freefem, gambit, geg, geomview,
ghemical, glpk, gnuplot, gperiodic, gri, gmt, gretl, lp-solve, mcl,
mpqc, multimix, rasmol, plotutils, pgapack, pspp, pdl, rcalc, xaos, XLisp-Stat and xppaut. (I'm just scratching the surface.) A free download is at UofW. It can be bought for $2.29 at ulnx.com. I'm still going through the disk. I didn't know there was this much free math software available. Xaos has the best real-time Mandelbrot zooming I've ever seen.
There are arbitrarily long progressions of primes. Eric Weisstein wrote a news article about it.
Material added 3 April 2004
Gathering for Gardner 6 was covered in today's New York Times.
William Gosper has a few copies left of his wonderful circle puzzle. It's made from beautifully cut, inch thick plastic. It was made by the geniuses at Puzzle Palace.
The monthly additions to the Puzzle Museum are well worth a look.
Patrick Hamlyn: "Robert Reid sent me
a very nice little manual puzzle which took several attempts over a
week or two before I got it. Using cardboard, plastic, neoprene,
high-density foam, icecream container lid or just paper: Cut out five
straight trominos and three U-pentominos in the same scale. Now cover
one set with the other. Real easy right? Everyone I've given it to
swears blind it's impossible. Some get it in a few minutes, many (like
me) take days or weeks. Here I reproduce Robert's 'spiel': COVER
- UP: As usual the politicians have bbundered; they are trying to
cover-up three twisted facts by five straight lies and they are getting
nowhere. Can you show them how it is done? There is only one solution. " [I got a copy of this as well -- it's a fantastic little puzzle.]
Berend Jan van der Zwaag: "How about Het Ding for unusual material making polyhedra? It's basically six telephone poles and many metres of steel cable."
Material added 30 March 2004
Minami Kawasaki: "My friend Shigeyoshi
Kamakura found the answer 23 (66*66)." Robert Wainwright:
"You may be interested in knowing that the recent Consecutive Square
posting (square sizes 1...23 within a square of size k= 66) exhibits
the "tightest" arrangement so far discovered. In correspondence with
Robert Reid last year, we arrived at a measure of "tightness" based on
the following: Sqrt[k^2 - (SUM 1^2 ... n^2)]/n. In otherwords,
the square root of the exposed area divided by the size of the square
enclosure. By this measure, Reid's n=43 (within a k=166 square) held
the record with a value of 0.25686+. Your recent posting has a
corresponding value of 0.24595+." This is an unexpected
correction for core sequence A005842. The conjecture that squares 1-26 can't fit into a 79x79 square seems weak, now. See also sequence A0081287.
Material added 22 March 2004
Bryce Herdt: It's good to have
something new for you. First, I have found a solution to the proportion
SEVEN/NINTHS = 7/9. I checked several fractions before finding a
doubly-true one. Has anyone else ventured into this arena? Answer.
Boris Alexeev, who discovered the very nice 2004 = 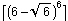 a few weeks ago, has won second place in the Intel Science Talent Search.
For his study into Automata, a frequent topic here, Boris has earned a
$75,000 scholarship. Congratulations, Boris!
a few weeks ago, has won second place in the Intel Science Talent Search.
For his study into Automata, a frequent topic here, Boris has earned a
$75,000 scholarship. Congratulations, Boris!
Erich Friedman:
722855133 has the peculiar property that all of its length 3 substrings
are divisible by 19. 722/19 = 38, 228/19 = 12, and so on.
For hand solvers -- find the largest number so that all length 2
substrings are distinct and divisible by 19. For computer
solvers, find the largest number so that all length 4 substrings are
distinct and divisible by
19. Is there a pattern to this? Can any number higher than
19 be used? Answer.
I took a look at the Asmus Schmidt method for complex continued fractions for a Math Games
column. Perhaps someone smarter than me can figure out that code
that generates each generation. Circles tangent to three others
is Apollonian packing,
and Eric has code for that. The other part is a circle with 3
points picked on the diameter, and one must find three circles tangent
to those given points and each other. Likely, one of the Triangle Centers
allows an easy answer. Another tact is to try looking at the
Moebius transforms of all circles in given generation, using the 8
special matrices Asmus Schmidt picked out. I'd like to see
generation 8 or so. Send Answer.
The following is a little puzzle by Oyler. Answer.


Simon Plouffe did an interesting analysis of approximations to physical constants.
Here is a peek at a Math Games column I'm
working on. I built a Great Rhombicuboctahedron with
supermagnetic spheres. Can you guess how their poles are aligned?
I'm looking for unusual materials for making polyhedra. If you
know of one, send me a note. I'll also be attending Gathering for Gardner 6, and hope to have a full report written by Monday.

Material added 12 March 2004
Nyles Heise: "In response to the $20 challenge posted on 6 July 2003, I've
built several wireworld implementations of a Turing Machine. I'm
including two of them here. The Turing machines do unary multiplications. I set out to do the
exact algorithm found in A. K. Dewdney's "The New Turing Ominibus", but
backed of slightly by leaving the original numbers on the tape along
with the product. The first design has 6 states plus halt and 4 symbols. It is
basically the Nich Gardner approach. That is, it has specific latches
to simulate the symbols on the tape. The symbols are read from and
written to the tape location under the R/W head. The shift register is
shifted either left or right one symbol. It's set up to do 4 = 2 X 2. The second design has 9 states plus halt and 2 symbols. This is
Karl Scherer's approach where the tape is simulated as a loop in which
electrons pass by the control mechanism and get modified as required.
It's set up to do 5 X 4 = 20.
Quite detailed descriptions of both machines are included in the .mcl
and viewable by clicking the blue information button." Well, that
will win it. You'll need Mirek's Cellebration to run these.

Michael Rios sent me an interesting
problem. What is the largest possible area of a quadrilateral
with sides 1, 2, 3, and 4? Answer.
If you can figure that out, try solving (2,3,4,5) and (3,4,5,6).
See a pattern? A general solution eludes me.
Oskar van Deventer has added the Tunable Maze to ClickMazes.com. You can tune this fractal maze while you are solving it.

George Sicherman is looking at the Polyiamond Exclusion
problem (which apparently has never been considered). He would
especially like to hear from anyone that can conclusively solve the
straight polyiamonds of length 3 and 5.
Eric Weisstein has started a page of Integer Sequence Primes.
If you happen to find a prime beyond what we have listed there, send us
details. Also, if you find a vast amount of nothing over a large
range, send us details about that, too. Anything new will likely
go into the Probable Prime database. Also, the Aspenleaf Concepts site lists many prime result lists.
Dick Hess has done some research into
Mixed Doubles tournaments. Two separate problems are of
interest. (1) Schedule a group of 4n doubles players on n
courts so they play as many rounds as possible without opposing or
partnering the same player twice. It's OK for partners in one
round to be opponents in another round. (2) The same as
above except there are 2n men (designated by odd numbers) and 2n women
(even numbers) that always play mixed doubles. The results below
will give you a flavor of this interesting problem. I look
forward to hearing from you and thank you for any help you can offer.
If you can improve these solutions, please let Dick Hess know
(ri(hislastname) at cox.net). Also, write me.
For
8 players there is a 3 round solution that holds for both problems and
even allows married couples (1 with 6, 2 with 5, 3 with 8 and 4 with 7)
to participate without ever playing with or against each other.
1: 1 2 3 4 5 6 7 8
2: 1 4 5 8 3 2 7 6
3: 1 8 7 2 3 6 5 4
For 12 players the situation is more interesting. I ran
exhaustive search computer programs and believe 4 rounds is maximum for
men's or ladies' doubles but only 3 rounds is possible for mixed.
Men's or ladies' doubles:
1: 1 2 3 4 5 6 7 8 9101112
2: 1 3 5 7 2 9 610 411 812
3: 1 4 6 9 2 8 712 3 51011
4: 1 71012 2 3 8 9 4 6 510
Mixed doubles:
1: 1 2 3 4 5 6 7 8 9101112
2: 1 4 5 8 3 6 912 7 21110
3: 1 611 2 312 5 4 710 9 8
For 16 players there is an elegant solution that allows us to schedule
8 married couples in 7 rounds so that spouses never play as partners or
opponents. The same solution works for men's doubles as well.
1: 1 2 3 4 5 6 7 8 9101112 13141516
2: 1 4 5 8 3 2 7 6 9121316 11101514
3: 1 6 914 3 81116 5 21310 7 41512
4: 1 81510 3 61312 514 9 2 71611 4
5: 11013 6 31215 8 5 41114 7 2 916
6: 11211 2 310 9 4 51615 6 71413 8
7: 114 712 316510 9 615 4 11 813 2
For 20 players the best I can do for mixed doubles is the 7 rounds
shown below. I have yet to explore the case for men's or ladies'
doubles. Nine rounds is the theoretical maximum but my search
program has only looked at a small fraction of the full set of possible
solutions.
1: 1 2 3 4 5 6 7 8 9101112 13141516 17181920
2: 1 4 5 8 3 2 7 6 9121316 11101720 15141918
3: 1 6 9 14 3 81116 5 21310 72019 4 15181712
4: 1 8 7 18 31015 4 5161120 9 21714 131219 6
5: 1 16 17 10 3141320 518 9 6 7 41512 11 819 2
6: 1 18 13 2 3 61910 5 41716 7121114 9 81520
7: 1 20 15 6 31217 8 5101914 7 2 916 11 41318
I put together a column on Number Games as part of my Math Games series. One thing I mentioned in the previous column was Artlandia's SymmetryWorks. Artlandia has just released Version 3.
Material added 29 February 
A new puzzle-maze by Oskar van Deventer, Lab Mouse, is now available courtesy of Henley Mob.
Jan Kristian Haugland has put together a series of Amazons puzzles, along with numerous other constructions.
The Metamath site
has a free set of handy mathematical symbols, 3000 proofs, and proofs
set to song. Lots and lots of formal proofs in HTML-rendered
abstract mathematical notation. A sample: 5
⊢ ((R1 ‘ A) ⊆ ∪x ∈ A
℘(R1 ‘ x)
→ ∀x(R1
‘ A) ⊆ ∪x ∈ A ℘(R1 ‘ x)).
A new Kuiper Belt object has been discovered. "2004 DW"
is estimated to be 1650 kilometers in diameter. Pluto, also in
the Kuiper Belt, is 2320 kilometers in diameter. This is the
largest solar system object to be discovered since Pluto.
Mathematician John Rainwater published an extensive number of papers, undeterred by his own nonexistence.
Henry Segerman has put together a very nice illustration of the Poincare Disk. You can also look at his Cantor Set, Entropy, Dodecahedron, Fractal, Mandelbrot, and other Autoglyphics. His Colloquium Posters are quite nice as well.
Material added 22 February 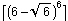
National Public Radio had a nice piece about Persi Diaconis and his coin flipping machine. (His home page)
If you flip a quarter and catch it in your hand, there is a 51% chance
it will land on heads. The report ends by saying that a coin at a
football game has different odds, since it is landing on the ground,
but the odds haven't been figured out.
I had a chance to listen to Bill Gates
during his High Campus Tour. UIUC was his first stop, and he's
going on to Harvard, MIT, and Carnegie-Mellon. He talked about
some of the computer science he's involved in. Bill Gates: "I've
been getting a lot of interest mail recently. I don't know if you are
getting some of these same offers. The most interesting ones say
that for just dollars a month, they will pay all my legal bills. I'm
not sure if I was the intended recipient for those. A few days
ago, my 7 year old came in and woke us to say that she'd been
trying out the computer. 'It's amazing!' she said. So I
said 'Okay. Keep using it.' But she went on. 'No, no, no! We Won! We
won money, dad!' I didn't want to say something flip like 'We
don't need more money' so I got up, and of course it was one of those
come-on type things, and there's my seven year old thinking she's won
some kind of amazing contest. I had to explain to her that it was
someone trying to get her to go to that website. We have a lot of
work in getting the computer to model our interests. What is worth
interrupting us for?" A great talk. If you'd like to hear it, write me, and I'll give you the address for a recording.
In 2001, I published Hamlyn's
Challenge. At the time, I was planning to have a major prize
contest, with the hexominoes sold in a nice cube. But I never
figured out how to get the 37 pieces made in a nice bakelite material
at a price anywhere near what I could afford. Barry Rawson just
solved what the contest was going to be.

Though I didn't get the hexominoes made, the R.G.B Round-up puzzle is made in bakelite, so it has that great feel, in addition to being a great puzzle.
Material added 14 February 2004
Erich Friedman suggests the annual puzzle
of writing the current year with a minimal number of one digit:
2^(22/2) - 2x22 = 2004. (333+3/3)x(3+3) = 2004.
((6+6+6)/6)x666 + 6 = 2004. 4^(4+(4+4+4)/(4+4)) - 44 =
2004. What are your best efforts for 0-9? Answers and Solvers.
Evan Variano and Paul Chaikin did a
study on random packings. Randomly placed spheres pack with
an average density of 64 percent. Randomly placed M&Ms pack
with an average density of 71 percent. The maximum density for
both shapes is 74 percent.
I put together a column on Guillochè
patterns as part of my Math Games series.
MathWorld has been redesigned. Also, A New Kind of Science is now available online.
Jorge Mireles has put together an applet
for studying snake-like length defined grid
spirals. He's made lots of discoveries with these.

Giovanni has put together his own page on polypolyomino
solutions. Colonel George Sicherman extended the problem to polypolyiamonds.
Both nicely extend the Livio Zucca
polypolyomino pages.
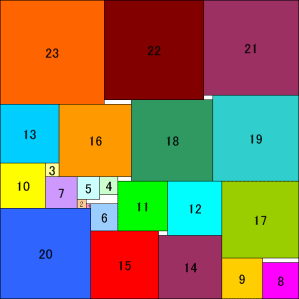
Phillippe Fondanaiche found a very
interesting solution for packing
squares of area 1-100.
Greg Dye pointed out to me some Flash
Optical Illusions at http://www.purveslab.net/ .
Andrea Gilbert recommended the Quantum TicTacToe applet.
A nice write-up about Tetris inventor
Alexey Pajitnov is available at BBC
News Online.
Material added 2 February 2004
Mary Youngquist Hazard has passed
away. She was the supreme solver of the National Puzzlers League, solving
every puzzle published for several decades. I remember one
transposal puzzle with the base haplomitoses/omphalosites that only she
could solve. Back in 1978, when I was much younger, she wrote to me
with some praise for one of my first efforts. In addition to being a
top-notch solver, she composed many puzzles and poems. Her most famous
puzzle is a poem:
Material added 1 February 2004

Older material
Anyone can subscribe to my moderated mailing list
at http://groups.yahoo.com/group/mathpuzzle/.
I announce updates to this site via that list.
01Dec03-22Jan04
07Oct03-18Nov03
25Aug03-30Sep03
06Jul03-17Aug03
01Apr03-29Jun03
25Dec02-26Mar03
29Oct02-13Dec02
03Sep02-21Oct02
16Jul02-26Aug02
13May02-09Jul02
04Mar02-06May02
05Dec01-25Feb02
19Aug01-04Dec01
17Feb01-05Aug01
02Jun00-11Feb01
More
Math
Puzzle Pages
Awards,
Book Recommendations, Chaos
Tiles, Characteristic Polynomial, ChebyshevU, Chromatic
Number of the Plane, Coin Weighing, Complex Numbers, Connecting
Dots, Crosswords, Digital
Sums, Dissecting Convex Figures, Domino Games, Encryption,
Eternity Puzzle, Fair
Dice, Gambling Odds, Graphs, Gravity, Guestbook, Golay
Code, Group Theory, Iamonds,
Knots, Leapers, Locales, Math Software,
Mini-Go, Multistate Mazes,
Number Fun, Parity,
Partridge Puzzle, Path
Problems, Pentagon Tiling, Philosopher Logic, Phonetic
Alphabet, Polyominoes, Prize Page,
Programs, Repeating
Decimals, Retrograde Analysis, Silly Puzzle, Similar
Dissections, Superflu, Stability of the Atom, Riemann Hypothesis, Tic
Tac Toe, Triangles, WGE123, Word Play, World Puzzle Championshiop 2000, Zome.
 |
 |
|
|
  |
 |
Martin Gardner celebrates math puzzles and Mathematical Recreations. This site aims to do the same. If you've made a good, new math puzzle, send it to ed@mathpuzzle.com. My mail address is Ed Pegg Jr, 1607 Park Haven, Champaign, IL 61820. You can join my moderated recreational mathematics email list at http://groups.yahoo.com/group/mathpuzzle/. Other math mailing lists can be found here.
All material on this site is copyright 1998-2004
by Ed Pegg Jr.
Copyrights of submitted materials stays with the contributor and is
used with permission.
 visitors since I started keep track. Yes, over one million.
visitors since I started keep track. Yes, over one million.