Material added 26 Jun 05
- The Icebox Maze
- Brian Smith: A few months ago you published my doppleganger maze. I really appreciate it. I have two new puzzles, both are rolling block mazes. The first puzzle uses three 1x1x2 rolling blocks in a 3x4 rectangle. Change ICEBXO to ICEBOX. Each end of a block has four copies of the same letter. Answer and Solvers.
-

- The second maze features an L-triomino as the rolling block. The goal is to move the block from the yellow squares marked 'ONE' to the blue squares marked 'TWO'. Gray squares represent unit cube barriers. The L-triomino can roll as long as it is not obstructed and the block is fully supported. The block can be positioned flat with all three of its cubes touching the ground level. It can be positioned so two cubes are at ground level and one pointing up. And it can be positioned so that one cube is touching the ground level and the overhanging cube is resting on a barrier block. For example, from the start the L-triomino can only move south. After moving south it can move west, which is a dead end, or east using the middle barrier block to support the overhanging cube. From there the block can move north, the other barrier is not in the way of the roll. Answer and Solvers.
-

- 2005 Digit Problem
- Erich Friedman: Find the 6 missing digits that make the equation (x^x + xx) / xx = 2005 true. Answer and Solvers.
- A Hookrug of Ten Different Squares
-
John Gowland: As I had left over cut wool from previous rugs, I thought I would make a scrap latch hook rug. However, to make it more interesting I made a rug with 10 different sizes of square. Perhaps people might like to work out what the different squares were. Answer and Solvers.
-

- Optical Illusions
- Michael Bach Optical Illusions and Visual Phenomenon is an excellent site.
- Plus.Maths.Org
- http://plus.maths.org features regular math articles. Their puzzle this month deals with three person nim.
- Divisor Puzzle
-
Vincent Lejeune: 487# 23# 13# 5^2 3^8 2^12 has the property that the sum of it's divisors is more than ten times the original number. What is the smallest number with this property? Answer and Solvers.
- A Hexomino Property
- Alexandre Owen Muniz: The square tetromino can be used to make two overlapping tilings of the plane such that all segments in the grid are covered by edges in exactly one of the two tilings. Finding the two hexominoes that have the same property was a nice puzzle.
-
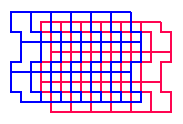
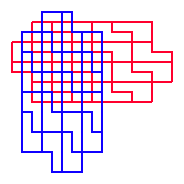
Material added 14 Jun 05
- U S Puzzle Championship this Saturday
- The U.S. Puzzle Championship will be held on Saturday June 18, 2005 at 1pm ET. Please read the rules and register before June 16, 2005. Even if you don't participate, the puzzles Nick Baxter has picked should be quite good.
- Mazes to visit this summer
- Robert Abbott: Since we’re all super-intelligent people (well, most of us are, right?) we scoff at conventional mazes that are printed in books and magazines—or put on paper place mats to keep small children amused at restaurants. Solving one of these mazes is a pretty dumb activity. But . . . have you ever been in a large, walk-through maze? Actually, most people haven’t. If the maze is done well, it can provide an exciting, even scary, experience. And solving it can be difficult, taking up to an hour or more. We become more involved in a walk-through maze than we do in any other work of art. So . . . here is: Mazes to Visit This Summer.
- A very popular Mirror Maze
- A mirror maze designed by Adrian Fisher - the world’s leading maze designer - has come second in a nationwide poll to find Britain’s best free attraction. King Arthur’s Mirror Maze at Longleat beat off stiff competition from the likes of Tate Modern and the National Railway Museum in York to take runner’s up spot in the survey, carried out by MSN Messenger. The maze, which opened in 1998 but only became a free attraction last year, was only pipped for the top spot by Big Ben and the Houses of Parliament.
- Sudoku as Featured Article
- David W. Wilson: Wikipedia's "Today's featured article" is about Sudoku, a Japanese number puzzle. The 3D Sudoku is quite interesting, as is the record-setting sudoku.
- Record Cunningham Chain
- Jiong Sun : I am happy to report the finding of record CC4
today:
953477584*5501#-1 Cunningham chain (8p+7) (2355 digits)
476738792*5501#-1 Cunningham chain (4p+3) (2354 digits)
238369396*5501#-1 Cunningham chain (2p+1) (2354 digits)
119184698*5501#-1 Cunningham chain (p) (2354 digits) - An Unexpected Packing
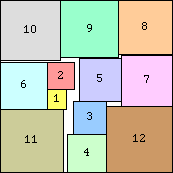
-
Erich Friedman: David Cantrell just found a packing of squares of AREAS 1-12 inside a square of AREA 81.
-
- Chesspiece Arrays
- George Jelliss: I've just uploaded four new issues to my "Games and Puzzles Journal", all dealing with chess-piece arrangement problems. Most of the material is not new, but I've not seen it treated systematically online before. There are a few results I think are new. Further results for inclusion will be welcome.
- DROD: Journey to Rooted Hold
- My latest column is about Deadly Rooms of Death. There is a huge variety of great puzzles in this game. The organization and presentation is better than in any puzzle game I've seen.
- Pentahex I and X
- George Sicherman: Andris Cibulis has done it again. Here is a common multiple of the I and X pentahexes.
-
Material added 02 Jun 05
- Hollywood magic done for real
- One classic piece of Hollywood fantasy involves taking a picture, and pulling a lot of detail out of it. A group of researchers from Stanford University and Cornell University have managed to pull this off. It works well enough that if you give them a picture of the back of a playing card, they can tell you what is on the front of the playing card, just from how light reflects off of the surrounding area.
- A Triangle Puzzle
- Bryce Herdt: I wanted to tell you about a new puzzle I put together. Its rules are simple; you have the triangular grid below, and you have to fit distinct triangular numbers into it across and down. Answer and Solvers.
-

- The K7 Knot puzzle
- If seven points are all connected to each other with string, there will be at least one one knotted loop with seven segments visiting each point once. I also learned about something called isomorphic factorization, which divides a graph into identical subgraphs. What graphs with 3 or 5 edges can you divide K6 into? It turns out K7 can be divided into 3 seven cycles. I combined these two facts. Divide the following K7 into three overhand knots. Answer and Solvers.
-
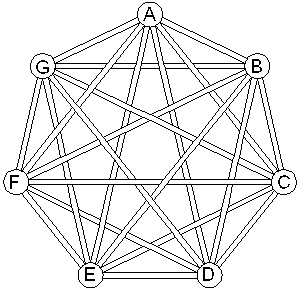
- The Turbulance of Chess
- Wiktor Macura: Thinking Machine 4 gives a chess game where the computer shows the moves under consideration in an aesthetically pleasing manner. The language behind the figure - Processing - is really cool. Processing is a variant of Java designed for image/sound manipulation.
- The Social Golfer problem
- Twenty golfers wish to play in foursomes for 5 days. Is it
possible for each golfer to play no more than once with any
other golfer? Yes, and you can find the answer to this and many similar questions at the recently updated Social Golfer problem page. - Advancement in the Twin Primes Conjecture
- Janos Pintz, Dan Goldston, and Cem Yildrim have made an advance in the study of small prime gaps. An explanation penned by Keith Devlin is available at maa.org.
- Consecutive Square packing
- Integer Sequence A081287 -- Excess area when consecutive squares of sizes 1 to n are packed into the smallest possible rectangle -- has been extended by Korf. The last one, packing squares of size 1 to 25 in a 43x129 rectangle, required 42 days of computer time. I believe a human solver can find the packing in 42 minutes. If anyone can find a zero in the extension of A081287, I'll pay $100. I used to think that was fairly safe bet. Guenter Stertenbrink looked at 31 squares, and his program needed 100 days to resolve the 93x112 rectangle. He found a better algorithm, now his program needs 54.4 seconds. Uh-oh. He found related papers at harvard, gatech, or.deis, citeseer, arxiv, math.tu, mai.liu, and cs.cf.
- Generalized Reptiles
- Erich Friedman's Math Magic this month generalizes reptiles in a very interesting way. Can you solve 411=33, or the other open problems? Last month's generalized square packing had some great discoveries.
Material added 23 May 05
- Martin Gardner's Mathematical Games
- Martin Gardner's Mathematical Games: The
Entire Collection of his Scientific American Columns -- is
now available for purchase
at maa.org! All fifteen books have been made into a large,
searchable PDF document. For example, I searched on the word Paris, and
got the following:
IN 1969, after 10 weeks of haggling, the Vietnam peace negotiators in Paris finally decided on the shape of the conference table: a circle seating 24 people, equally spaced. Assume that place cards on such a table bear 24 different names and that on one occasion there is such confusion that the 24 negotiators take seats at random. They discover that no one is seated correctly. Regardless of how they are seated, is it always possible to rotate the table until at least two people are simultaneously opposite their place cards? (Mathematical Circus, ch 15)
The disk contains the following books:- Hexaflexagons and Other Mathematical Diversions
- The Second Scientific American Book of Mathematical Puzzles and Diversions
- New Mathematical Diversions
- The Unexpected Hanging and Other Mathematical Diversions
- The Magic Numbers of Dr. Matrix
- Martin Gardner's 6th Book of Mathematical Diversions from Scientific American
- Mathematical Carnival
- Mathematical Magic Show
- Mathematical Circus
- Wheels, Life, and Other Mathematical Amusements
- Knotted Doughnuts and Other Mathematical Entertainments
- Time Travel and Other Mathematical Bewilderments
- Penrose Tiles to Trapdoor Ciphers
- Fractal Music, Hypercards, and More Mathematical Recreations from Scientific American
- The Last Recreations: Hydras, Eggs, and Other Mathematical Mystification
- Star Wars puzzle
- The National Public Radio weekly Sunday Puzzler is mine this week. What word has the letters of STAR WARS in order? No, the word isn't "starwards." If you can find the answer, send it to National Public Radio for a chance at various prizes.
- 2005 Google U.S. Puzzle Championship
- A chance to get on the U.S. Puzzle Team happens Saturday June 18, 2005 at 1pm ET. Details. The team will compete at the World Puzzle Championship.
- Fair Dice column
- My latest column for maa.org was about Fair Dice.
- U and X pentahexes are compatible
- George Sicherman: Andris Cibulis has just found a common multiple of the U and X pentahexes.
- webMathematica Wiki
- Mathematica-users.org is a wiki-based website for Mathematica users. Anyone can contribute. All of the contributed notebooks are also viewable as HTML pages.
- Three Digit problem
- Each day, three digits are chosen at random. How many days would one need to wait to expect to see a number that had repeated digits, like 434, 888, or 551? In Sacramento, such a game lasted for 100 days.

Material added 13 May 05
- Finite Simple Group (of Order Two)
- The Klein Four Group is the premiere a capella group of the world of higher mathematics. Their music site is hosted at the Northwestern University mathematics department. In addition to listening, you can also get song lyrics.
- Walter D. Pullen's Fractal Maze Generator
- Mark Wolf developed the first Fractal Maze. Now, Walter Pullen of Think Labyrinth! has added a fractal maze generator to his free program Daedalus. Can anyone solve the following maze? Answer and Solvers.
- Rieselsieve
- The Rieselsieve project has announced that 234847*2^1535589-1 is prime. The Riesel primes should be cracking into the top 20 primes, with the next discovery.
- The "All Five" Puzzle, and other news stories
- Kepler tried to model the solar system on 5 nested platonic solids. Wayne Daniel of interlockingpuzzles.com has managed to make a puzzle on this same theme, and the New York Times wrote a column about it. BBC News recently wrote about the Rock Paper Scissors match between Sotheby's and Christies. The New York Times also told the story of how Fortune Cookies rattled the Powerball Lottery.
- V and X pentahexes are compatible
- George Sicherman: Andris Cibulis told me he was sure that the V and X pentahexes are compatible. I just found out that he was right!
- Numb3rs, CSI, and Christopher Lee
- In my Numb3rs column, I said it was remarkable that all primary actors were exactly one link away from Christopher Lee (the center of the Hollywood Universe). Kevin J Compton took me to task for using the size of the full database -- since all the actors in a given show are in play at the same time, it's actually much more likely. To prove it, he showed that all 8 primary actors of CSI are exactly one link from Christopher Lee.


Material added 05 May 05
- 05/05/05 is the 5×5×5th day of the year.
- It's a great day for those who like 5's. For lovers of 6, though, things aren't so great. The Number of the Beast, 666, has been downgraded to 616 after a more careful examination of the original source material.
- Balanced Consecutive Tilings
- Erich Friedman's Math Magic this month concerns packing consectutively sized squares into a rectangle. He's added a prize, too. Many interesting discoveries have been this month at Math Magic.
- Busy Beaver competition
- About a year ago, I pointed out that no significant advances had been made in the Busy Beaver Turing machine problem for about 15 years -- a long time for a problem that deals with computer searches. Terry and Shawn Ligocki have been looking at the problem for a few months, and have set five records. You can see the current record-setters at The Busy Beaver Competitions page.
- Recent Physics news
- A new type of fusion has been discovered. Two entangled atom clouds have been observed. Finally, a movie of the r-process of element creation has been made.
- Another way to get Fibonacci
- Richard Guy: "It's well-known to those who well know it that 1/999998999999 = 0.000000 000001 000001 000002 000003 000005 000008 000013 000021 000034 000055 000089 000144 000233 000377 000610 000987 001597 002584 004181 006765 010946 017711 028657 046368 075025 121393 196418 317811 514229 8320413462711783125245837028962...." Very interesting. You might try to figure out what 1/4999999999 gives.
- DROD: Journey to Rooted Hold
- I've lately been enjoying the puzzle game DROD: Journey to Rooted Hold. You can get the free version of the game as well, from there, drod.net, or Sourceforge.

Material added 24 April 05
- Fractal Food
- John Walker has written a column on the beautifully fractal chou Romanesco. He did some fractal zooms on the vegetable, with many photographs.
- A nicely distributed sequence
- Bernardo Recamán: The set of consecutive positive integers 2, 3, 4, 5, 6, 7, 8, 9, and 10 use, altogether, each of the digits 0 to 9 exactly once. Find another set of two or more consecutive positive integers that, together, use each of the digits 0 to 9 exactly the same number of times. Answer and solvers
- Packing challenges, Serhiy's puzzle book
- Erich Friedman has added three new packing challenges: triangles in hexagons, circles in tans, and tans in circles. Serhiy Grabarchuk has been finding improvements, so perhaps you can find some, too. Incidently, Serhiy has a great new puzzle book that everyone should get: The New Puzzle Classics: Ingenious Twists on Timeless Favorites.
- Interesting words
- Denis Borris: The following six three-letter words share an interesting property: ELM OIL FEE GOT MOD TUM. What is it? And what is the seventh word to have this property? Answer and Solvers.
- PQRST 13
- PQRST 13 starts on April 23rd, Saturday at 20:00 (GMT+02).
- Nob Yoshigahara Puzzle Design Competition
- If you have an interesting mechanical puzzle design, consider entering it in the 2005 Puzzle Design competition. Further details, along with details of the last five competitions, can be seen at puzzleworld.org.
- New wooden puzzles
- Some of the items that might be at the design competition are the new Stickman Boxes, available at cubicdissection.com (top quality). A site I know little about is lookina.com, which makes Wooden House Puzzles (unknown quality).
- Bureaucratic maze
- Wei-Hwa Huang successfully used Robert Abbott's Bureaucratic maze to kickoff the 7th Bay Area Night Game. Robert Abbott has a writeup at logicmazes.com.
- Capturing the Unicorn
- A high-quality scan of the tapestry Capturing the Unicorn was attempted by the Met. Unfortunately, after it was taken down so it could undergo many separate photographs, to be later assembled, the material started relaxing, causing all the photographs to be slightly misaligned. Nothing beyond the abilities of two mathematicians, in this case Gregory and David Chudnovsky. A full story is in the The New Yorker.
- Horoball diagrams of knot complements
- Nice pictures of knots can be seen at Morwen Thistlethwaite's home page. Somehow, knot inverses can be represented by horoballs. According to the site, the centers and radii of the horoballs were computed by Jeff Weeks's program SnapPea, and rendering was accomplished using Larry Gritz's Blue Moon Rendering Tools.
- Recurrence Plot of the Day
- For those of you with a daily need for recurrence plots, there is now a site for you, with a Recurrence Plot of the Day, for all your nonlinear data analysis needs.
Material added 15 April 05
- Isosceles Right Triangles in Circles
- Erich Friedman has added a new page to his Packing Center: Tans in Circles. The page includes diagrams of five new packings, which Eric found this month. He is looking for improvements.
- Math Games: Chessboard Tasks
- My latest column is on Chessboard and Grid tasks. I like staying cutting edge on these topics, so I was quite pleased to receive a note from Guenter Stertenbrink a few hours after my column went live, about progress with the Queens graph. The queen graph has been proven impossible for 2, 3, 4, 6, 8, 9, 10. Solutions have been found for all other cases up to 25. The state of the order-26 queen graph is unresolved. It is hypothesized that the queen graph is solvable for all n>10.
Material added 09 April 05
- Goldbach's conjecture
- I played around with Goldbach's conjecture a few days ago, and made a list. 3 and 5 are necessary for 3+5=8. 7 is necessary for 5+7 = 12. 11 seemed to be completely unnecessary, though, so I pulled it out. 13 is then needed for 5+13 = 18 (can't use 7+11=18, since I've ruled 11 unnecessary.) And so on, looking at each prime, and determining whether they are necessary or unnecessary. Jacques Tramu confirmed and extended my results. The following primes seem to be completely unnecessary, up to 60000. 11 17 29 41 59 67 71 73 89 97 103 127 137 149 151 163 173 179 181 191 193 197. You might enjoy looking for the sum for 208 that avoids unnecessary primes. Steven Stadnicki extended this to a million. His list and program are here (2meg zip). If you can find a pattern to this, and prove it works, that would be a proof of Goldbach. Followup: Johan Claes has extended the list of necessary primes to 2 billion. "A very interesting property is that they can be efficiently calculated with a sieving process." So, this might be a method for extending the Goldbach verification to 10^20, with a year of computer time. Zip of the List.
- Chris Cole
- The Escher configuration of a 3-cube compound creates 67 different cells. Is this the best possible? [You might enjoy the Adaptive IQ Test that Chris helped to put together.]
- Kai G. Gauer
- An interestingly difficult Kriegspiel problem by Geoffrey Foster is available. A Kriegspiel applet is available.
- Chomp
- Eric Friedman and Adam Landsberg have proven the 3×n game of Chomp always has a unique first move. See their paper at ftp://ftp.orie.cornell.edu/pub/techreps/TR1422.pdf .
- Stable Tents contest
- Erich Friedman has turned 40, and is doing a contest on stable tents at Math Magic. You can see the current records for the problem.
- Densest Packings of Equal Spheres in a Cube
- Hugo Pfoertner has made a page of the Densest Packings of Equal Spheres in a Cube.
- Math License Plate Contest
- The Math License Plate Contest yielded some nice plates. (Mine is MTHPZZL, as it turns out.)
- Page of Math Errors
- The Page of Math Errors is good material.
- Mafia
- For Chess, Go, or organized sports, people often get high quality components to enhance the game. One of my favorite games, Mafia (Princeton rules, NTNU rules), is now available as a nice card deck as The Werewolves of Miller's Hollow.
- Rudolf Schöning
- In the early 80's, I came across the game of Morpion in the French magazine 'Jeux & Stratégie'. They gave a 170 move solution that was found by hand. This solution is available at the site. It appears that no progress has been made in 20 years. Do you happen to know about any progress, or could you direct me to a place where I can discuss this game? I am also interested in the general solution, i.e. the maximum number of moves for an arbitrary pattern of N given points. [I don't know of any progress.]
- Largest Factor Ever Found by the ECM Technique
- A factor of 3466+1 has been found: 709601635082267320966424084955776789770864725643996885415676682297. It's the largest factor ever found by the ECM technique. Other large factors are maintained by the Cunningham project.
- Good Math Books
- I'm always looking for good math books. One recent find was the Handbook of Mathematics by Bronshtein, Semendyayev, Musiol, and Muehlig. I'd actually seen this book before in a German edition,a language I do not know. As I paged through it, I thought "wow, this is a good book." I just recently found the English edition.
- NYT Marks 100th Anniversary of Einstein's Most Famous Paper
- The New York Times devoted an entire page to Physics on the subject of the 100th anniversary of Einstein's most famous paper.
- Multiple-unit Dodecahedral Constructions
- If you have too many dodecahedra, you might try making some Multiple-unit Dodecahedral Constructions.
Material added 01 April 05
- MathForge Surprise
- Imagine my surprise when I visited MathForge just now.
- Tiled CA
- Brian Prentice: I enjoy reading your Math Games pages and exploring the ideas that you illustrate. Here is a program that your readers may find interesting: Tiled CA. This program runs cellular automata simulations on a large number of grids which can be constructed from various shaped tiles. These tile shapes can be triangles, squares, parallelograms, pentagons, hexagons or octagons. A grid editor is included with which new grid definitions may be constructed or existing grid definitions may be modified. Are there any grids for which there is no rule supporting gliders? [Tiled CA is the most gorgeous Windows program I've seen in awhile.]
Material added 29 March 05
- Math Games: A Zillion Connection Games
- My latest Math Games column concerns Cameron Browne's book Connection Games, as well as the game engine Zillions of Games. I hadn't looked at the ZOG site carefully in awhile, and was quite pleased to see the well-organized game list as I started writing. The column has my usual gaggle of links to other neat places. One site I didn't know about was the complete solution to 7x7 Hex.
- Game of Life: 17c/45 Caterpillar Spaceship
- A new speed has been found for a spaceship in the Game of Life: The 17c/45 Caterpillar spaceship. To watch it in action all at once, you'll need a 4195x330721 pixel monitor. It was discovered by Gabriel Nivasch, Jason Summers, and David Bell. See Eppstein's page for other glider news. You can also see his paper Searching for Spaceships (PDF) in the online book More Games of No Chance.
- Friedman's Tangrams Pages
- Erich Friedman has starting two new packing pages, Tans in Squares, Squares in Tans, and Tans in Tans. If you can improve any of these, write to Erich. On the Tans in Tans page, you'll see that I improved on his first result for 3 tans in a tan. I knew it would be a good puzzle, the answer there isn't the best possible, numerically. Can you sort through the simultaneous equations and find the exact solution? Answer and solvers.
- Y-pentomino 12-Fold Replica
- One long unsolved problem has been whether the y-pentomino could make a 12-fold replica of itself. Patrick Hamlyn hates unsolved polyform problems. His polyform solving program can usually find solutions in microseconds. Here, it took "116 hours, 296 million 'off-by one' partials, 41 billion piece placements." Still unsolved is why this particular problem was so difficult, and why this particular solution worked.
- Sums of Powers
- Somewhere, I discuss the x^3 + y^3 = z^2 problem. I recently learned of Dario Alpern's Sums of Powers page. For an older puzzle, try the following (Answer and Solvers):
- Flexagon Discovery
- The hexadodecaflexagon has been discovered.
- Knight Problem
- Melvyn Knight once asked about solutions to N = ( x + y + z )*( 1/x + 1/y + 1/z ). For example, with N=103, the smallest solution is x=14156395253, y=-131237206100, z=1736693066100. For a much harder problem, try N=888. Some numbers don't have solutions, such as N=5. Using elliptic curves, it was possible to isolate all the N which might have solutions. After a multi-year search, every number from -1000 to 1000 has been resolved in the Knight problem.
- Snub Cube
- You probably know that most of the regular polyhedra are closely related to the golden ratio, or Fibonacci constant. Did you know that the Snub Cube is related to the tribonacci constant? It was news to me.


Site Goals
Martin Gardner celebrates math
puzzles and
Mathematical Recreations. This site aims to do the same. If you've made
a good, new math puzzle, send it to ed@mathpuzzle.com.
My mail address is Ed Pegg Jr, 1607 Park Haven, Champaign, IL 61820.
You can join my moderated recreational mathematics email list at http://groups.yahoo.com/group/mathpuzzle/.


 visitors since I started
keep track.
visitors since I started
keep track.