Fair Dice, Iamonds, Eternity, Mazes, Atom Stability, Dissections, Kites&Bricks, Triangles, Retrograde, Pentagons, Prize Problems, BOOKS, LINKS, Chaos Tiles, and Partridges.	www mathpuzzle
Mathematica	Mathematical Explorer	MathWorld
mathforge.net	Math Games

Material added 28 Jun 2004

The great puzzlemaster, Nob Yoshigahara, has passed away.  He helped both me and this site out a lot in the past few years, and I'm just one of hundreds of puzzlemakers he has helped, and one of the millions of puzzler solvers he has entertained.  My latest Math Games column is about him. 

Serhiy Grabarchuk: "Thank you very much for such a great article about Nob! I'd like to add that past year there was one very remarkable milestone in Nob's life. In 2003 (May 17, 2003) Nob received the Sam Loyd Award for Lifetime Achievement at that year's Association of Game & Puzzle Collectors (AGPC) Convention in New Haven. As he wrote to me about that Convention and Loyd Award receiving: "There was a paradise on this earth!" Some pictures from the New Heaven AGPC Convention (including several with Nob) you can find in the pages of the Games and Puzzles Gallery - AGPC Album at Bruce Whitehill's Big Game Hunter website.

Several people sent me puzzles for the contest I mentioned on 13 June.

1. David J Bush sent me some some difficult 12x12 Twixt puzzles.
2. Michael Rios:  I am dissatisfied with the meager number of possible opening moves for white in a standard game of chess.  I rearrange the 16 pieces I have, still keeping them all confined to the first two ranks, such that I now have the maximum number of unique first moves that I can have.  (Of course, I don't want to destroy the charm of the game, so pawns in the first row still have their normal two first move options.  Too bad for those pawns in the back row, eh?) What's that arrangement?
3. Andrew Buchanan: On an otherwise empty chessboard, how many distinct legal routes are there for a king to move from a1 to h8 in n moves? (He also sent the solution).
4. At Freshmeat.net, Steven Atkinson has posted a polyform program, along with the complete source code. (freshmeat.net is a primary place for source code of all types)
5. Mark Heim: Here's a puzzle based on Falling Polyominoes, a combinatorial game invented at Mathcamp last year by me and small group of people who were interested in game theory. The rules are simple: Left is allowed to move any single polyomino that is either green or blue, and Right is allowed to move any single polyomino that is green or red. A move consists of sliding a polyomino of the appropriate color either down or left for at least one unit. If a polyomino runs into another polyomino or into a black wall, it cannot be moved any further. Also, during one move, a polyomino cannot change direction. The puzzle is to determine the winner, assuming both players play perfectly and also assuming that Left moves first. An equally challenging puzzle is to determine who wins if Right starts.

Cihan Altay: Puzzle Design Tournament 2004 has ended. You can download the optimization puzzles, see the results and best answers submitted, on the tournament website: http://www.otuzoyun.com/puzzledesign/.

The puzzle set for the 2004 Google U.S. Puzzle Championship is well worth trying out.  I especially like the new puzzle types by Erich Friedman.  Longtime solver here Joseph DeVincentis is now on the US Puzzle Team.  Congrats!  Have fun with Wei-Hwa in Opatija, Croatia.

My next major conference will be the Wolfram Technology Conference.  For anyone that comes, I'll be glad to show my collection, lots of math stuff, and our Periodic Table Table. 

There is a special Issue of  TCS about "Combinatorics of the Discrete Plane and Tilings". Theoretical Computer Science, Volume 319, Issues 1-3, Pages 1-484 (10 June 2004)

An article on computational origami was covered on Slashdot.  The Particle Data Group blue book will be sent out in August. It's a free book -- add your name to the mailing list if you have any interest in particle physics.

Patrick Hamlyn took a look at the 1248 enneominoes without holes.

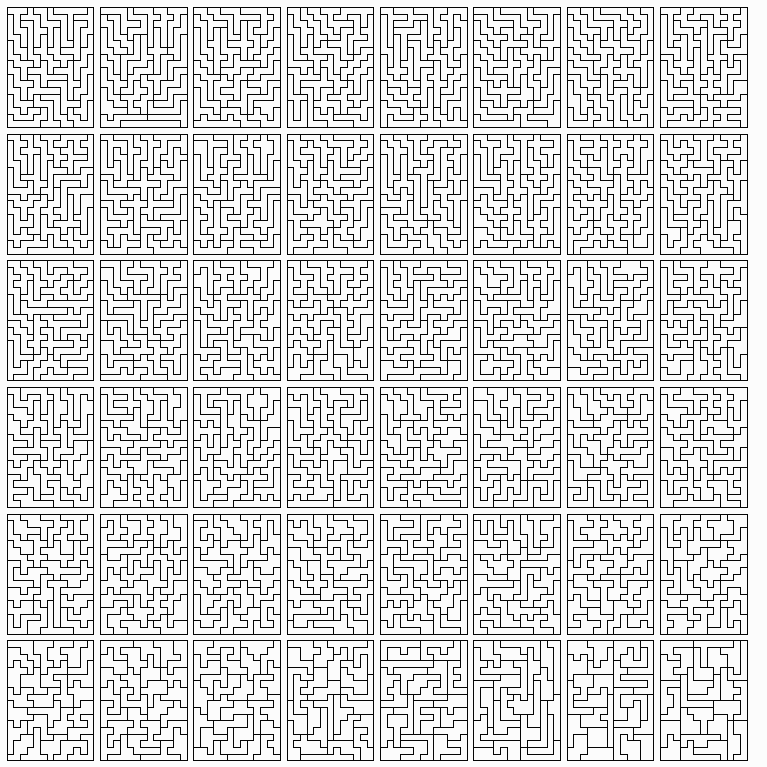
Material added 13 Jun 2004

http://wpc.puzzles.com/ -- The U.S. Puzzle Championship will be hheld on Saturday June 19, 2004 at 1pm ET. Please read the rules and register here before June 17, 2004.  Some warm-up puzzles can be seen at Conceptis.  A whole book of these is the World Puzzle Championships Omnibus.

Over 25 years ago, Elwyn R. Berlekamp, John H. Conway, and Richard K. Guy set out to make the definitive book on the mathematics of Games.  They succeeded with their book Winning Ways.  It went out of print, and became quite valuable.  Now, Winning Ways is now back in print entirely.  Volume 1, Volume 2, Volume 3, and Volume 4 are all available.  I have one extra copy of Volume 3, which I will give to whoever sends me the best game-related puzzle. Send Puzzle.  On Numbers and Games is also available.

My latest Math Games column features 2D Turing Machines.  My next one is about Egyptian Fractions -- if you have something really neat concerning Egyptian Fractions, please send it to me soon.  Another column I'm working on involves hemispheres.  I hear the word "Hemi" in car advertising too often to avoid a long explanation.  If you know any good hemisphere puzzles or trivia, please let me know about it. For future columns, I'm pondering moire patterns, the 12 queens problem, optimized paths, the projective plane, venn diagrams, word lists, golf tournaments, mobile mechanics, interactive fiction, hyperbolic tiling, iamonds, pi via billiards, k7 knots, folding tetrahedra, Harary's Pathos, and modern burr puzzles.  Write me if you have any comments, ideas, or suggestions for future columns, or corrections to past columns.

There is a very nice paper on Heesch's Tiling Problem in the latest American Mathematical Monthly by Casey Mann, the University of Texas at Tyler tiler. Perusing MAA Focus, I found out about their new Convergence webpage.

William Paulsen's Calculator Maze is very nice.

If you're curious about the shapes of dice that have actually been made, dicecollector.com has a full page about them.  I'd like to learn more about the 32-sided Czechoslovakian roulette die.   With rapid prototyping, some metal hexecontahedra could be made as a small project by one of you.  If anyone does, let me know, and I'll post your email address here so you can take orders.

Material added 05 Jun 2004

The Bureaucratic Nightmare is a maze through red tape.  Robert Abbott: "Just wanted to let you know that there is now an interactive version of the Bureaucratic Maze that you can play on-line. It's called the Bureaucratic Nightmare and it was created by Eric Shamblen. To try it, go to my home page: http://logicmazes.com/ then go to the "What's new" banner at the top, and follow the pointer."

I'll be attending the Wolfram Technology Conference in Champaign IL on October 21-23.  I'll be glad to show my puzzle collection and the periodic table to anyone attending.

Material added 29 May 2004

2^24036583 - 1 is prime.  A full news release on the discovery can be seen at mersenne.org.

Material added 23 May 2004

Jan Kristian Haugland is offering $100 in potential prizes to people that can better his current finds in Grid Subgraphs.

Jean-Charles Meyrignac:   Just to mention that I recently (11/11/2003) found a 9x8 grid with french words. In France, it's considered as the Holy Graal by crossword makers (verbicrucistes in french) !  List of Definitions.

D E C R O C H E S
E C O E U R A N T
R O N F L A N T E
A T T R I S T E R
P A R A P H E R A
E M A C I E R A S
R E I T E R A I S
A S S E N A S S E

I've added a page on Roger Beresford's Gallery of Cubic Graphs.  He's developed a very interesting notation for nice graph presentations.

A possible Google Puzzle Group is here... google groups 2 is in Beta testing.

I found a stable magnet configuration that's quite pleasant.

Erich Friedman: Find a 83-omino that contains exactly 2004 rectangles of various sizes.  Send Answer.

I used 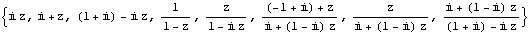, the 8 Moebius Transforms for Complex Continued Fractions, to make the following picture. It all starts with the three number on the complex plane {0, 1, 2}.  Three complex numbers will define a line or a circle.  Let one of the 8 transforms act on those three complex numbers, and you'll get three new numbers that define a line or circle.  The below picture shows some of the ways of using up to 5 of the transforms on{0, 1, 2}.  Piers Haken -- "I’m fascinated by the short piece you wrote on the relationship between klenian groups and complex continued fractions. I have written a program to do a real-time zoom into an appolonian gasket using soddy circles and I’d love to extend it to the Gaussian numbers."  Turns out that the math is pretty simple.

Material added 13 May 2004

Nyles Heise has built Langton's Ant in Wireworld, along with many other things.  He also built a lovely Binary Counter (as explained at Mathworld).  They are incredible to watch.

I made a Mathematical Crossword for my latest Math Games column, along with a run-down of the rules and records I know about.

Cihan Altay: PDT 2004 is starting. Send your optimization puzzle until May 21st to compete. See the Rules&Progress of the tournament on the tournament web site:  http://www.otuzoyun.com/puzzledesign/

The Math Underground has started up, with math t-shirts, and some other stuff.

John Grint:  I have a number of identical rectangular sheets of paper.  The sides and diagonals of each sheet measure an exact number of millimetres, and the sheets are less than 1 metre on each side.  I can place a number of sheets side by side to make a long rectangle whose diagonal is also an exact number of millimetres; alternatively, I can join a (different) number of sheets top to bottom to make another long rectangle whose diagonal is again an exact number of millimetres.  How many sheets of paper do I need to make each of the long rectangles?  (Send Answer)

Brad Pitt was recently asked about the injury to his Achilles tendon.  He damaged it severly enough to cause a delay in shooting, while playing Achilles.  "Stupid irony," Pitt mumbled dismissively.

Material added 3 May 2004

My write-up on the Quantian Distribution has lots of good information.  Many of the packages in Quantian are interesting to play with, such as the Surface Evolver by Ken Brakke, which is an interactive program for the modelling of liquid surfaces shaped by various forces and constraints.  A good windows program is Irfanview 3.91, which will open any image format very quickly.

Math Forge has added MathML, and it works quite nicely.  The Math Underground has started, which has some math t-shirts. The Mathematical Fiction site lists references to math in works of fiction. Erich Friedman sent a puzzle based on his latest Math Magic experiment" "Place the digits 1 through 9 in a 3x3 grid with the operations of addition, division, and exponentiation in between the digits to produce 3 horizontal and 3 vertical expressions, all of which are equal to 16.  Likewise, use the digits 1 through 9 with only the operations of addition, subtraction, and exponentiation to give every column and row equalling 7.  Both solutions are unique, up to reflection."

Wei-Hwa Huang and I attended Mensa Mind Games in Chicago.  He's a self-described crazy gamer, and to show his credentials he played and reviewed every game. My thoughts coincide with Wei-Hwa's pretty closely.  My favorite game there was The Penguin Ultimatum, which was fun, original, deep, and disarming.

Rick Shepherd has solved my Chaos Tiles challenge.

Material added 19 April 2004

Robert A Hearn:  "Place four coins on the bottom row of circles (G, D, E, and R), so that the letters MARTIN are exposed.  Your challenge is to slide these coins along the graph edges, covering the top row of circles, to expose the letters GARDNER.  Easy, right?  There's a catch -- at no time are two coins allowed to be next to each other along an edge.  You'll find this makes the task much more interesting.  (And yes, you have to slide the coins one at a time, all the way from one circle to another!)  For example, the G coin cannot move, initially -- it would wind up adjacent to the D coin.  But D can move to T.  (or D-T).  Be careful to pay attention to all edges as you slide the coins -- the I-R edge is particularly easy to miss.  Good Luck!"  Answers and Solvers.

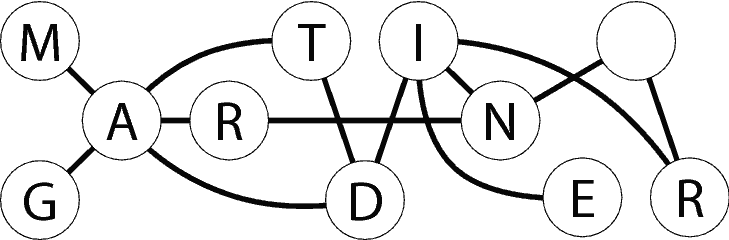
The Martin Gardner coin puzzle, by Robert A. Hearn.

A new column on Integer Complexity is at Math Games.

Minami Kawasaki:  "Mr.Yasushi Ireimake has written a fast program for solving the problem of consectutive squares in squares. This program can find the answer of  23(66*66) less than 10 seconds."

Berend Jan van der Zwaag: "Thank you very much for the puzzle!!!  I like it very much. It arrived on Friday. My wife called me and said "there is a VERY LARGE package for you!" She had no idea what was inside. :-) The puzzle is even more beautiful (and much bigger :-)) than I expected.  Please thank Kate for me for her beautiful piece of artwork."   Kate Jones: "Thanks for adding our link to your 37-squares citation. I have now made up a special page for them and would appreciate your putting the full URL so people interested in ordering can find it immediately: http://www.gamepuzzles.com/37square.htm"  Only three sets remain.  Robert Reid and Berend Jan van der Zwaag both solved placing squares of size 1-37 in a 133x133 square independently.

Older material
Anyone can subscribe to my moderated mailing list at http://groups.yahoo.com/group/mathpuzzle/.
I announce updates to this site via that list.

01Feb04-13Apr04   01Dec03-22Jan04   07Oct03-18Nov03   25Aug03-30Sep03   06Jul03-17Aug03   01Apr03-29Jun03   25Dec02-26Mar03   29Oct02-13Dec02   03Sep02-21Oct02   16Jul02-26Aug02   13May02-09Jul02   04Mar02-06May02   05Dec01-25Feb02   19Aug01-04Dec01   17Feb01-05Aug01   02Jun00-11Feb01 

More Math Puzzle Pages
Awards, Book Recommendations, Chaos Tiles, Characteristic Polynomial, ChebyshevU, Chromatic Number of the Plane, Coin Weighing, Complex Numbers, Connecting Dots, Crosswords, Digital Sums, Dissecting Convex Figures, Domino Games, Encryption, Eternity Puzzle, Fair Dice, Gambling Odds, Graphs, Gravity, Guestbook, Golay Code, Group Theory, Iamonds, Knots, Leapers, Locales, Math Software, Mini-Go, Multistate Mazes, Number Fun, Parity, Partridge Puzzle, Path Problems, Pentagon Tiling, Philosopher Logic, Phonetic Alphabet, Polyominoes, Prize Page, Programs, Repeating Decimals, Retrograde Analysis, Silly Puzzle, Similar Dissections, Superflu, Stability of the Atom, Riemann Hypothesis, Tic Tac Toe, Triangles, WGE123, Word Play, World Puzzle Championshiop 2000, Zome.

EXCELLENT SITES AND PRODUCTS

Mr. Puzzle

MORE SITES

Martin Gardner celebrates math puzzles and Mathematical Recreations. This site aims to do the same. If you've made a good, new math puzzle, send it to ed@mathpuzzle.com. My mail address is Ed Pegg Jr, 1607 Park Haven, Champaign, IL 61820. You can join my moderated recreational mathematics email list at http://groups.yahoo.com/group/mathpuzzle/. Other math mailing lists can be found here.

All material on this site is copyright 1998-2004 by Ed Pegg Jr. Copyrights of submitted materials stays with the contributor and is used with permission.
visitors since I started keep track. Yes, over one million.