Fair Dice, Iamonds,Eternity, Mazes, Atom Stability, Dissections, Kites&Bricks, Triangles, Retrograde, Pentagons, Prize Problems, BOOKS, LINKS, Chaos Tiles, and Partridges.	www mathpuzzle
Mathematica	Mathematical Explorer	MathWorld

Material added 18 November 2003

Puzzle of the week.  In a chess game, White's sixth move is g×f8N++.  Reconstruct the game. Answers and Solvers. Noam Elkies and Richard Stanley verified that this is the longest game uniquely determined by a single move. I found it in the October 2003 Emissary, a publication of msri.org. The problem dates back to 1994, was found  by Peter Rossler, and can be found on his personal page. It was also the Christmas 2000 puzzle at Chessbase.

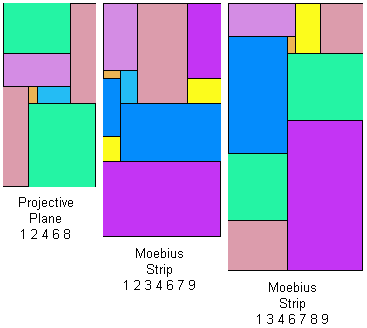
My fourth Math Games column for maa.org talks about the Loculus of Archimedes, the world's oldest puzzle, and the complete solution for it that was recently found by Bill Cutler.  The column made Slashdot. It's been a busy week for solutions to long-unsolved problems.  At MathWorld, you can read about the perfect order-5 magic cube that was just recently discovered by Walter Trump and Christian Boyer.  At Mersenne.org, you can read about the new largest prime, the 40th Mersenne prime.  Giovanni Resta has made a page on Perfect Rectangles. Patrick Hamlyn found some perfect dominoes on the Moebius strip and projective plane. 

The McGurk effect is a very convincing audio-visual illusion.  If you watch the short video, you will hear one thing.  If you close your eyes, you will hear another.

Small Fractal Maze by Mark J. P. Wolf (mark.wolf at cuw.edu).  Graphically simpler than the fractal maze posted last month, but still difficult and multiply recursive.  Color has been added to make the pathways clearer, but it is only decorative (although fractal mazes with color rules are another possibility).  The fractal maze also walks the line between traditional mazes and multi-state mazes, in that it is presented as a multi-state maze only because of its recursive nature; on a screen of infinite resolution, copies of the maze could all be drawn in and the boundaries between them erased, leaving a traditional over-and-under maze, albeit one of infinite detail.  Question: Since traditional mazes can be solved by the “left-hand rule” (or some variation of it for over-and-under mazes or three-dimensional mazes), is there any solving rule that a person wandering through a fractal maze could use to solve it?  Answer and Solvers.

Small Fractal Maze by Mark Wolf.

A new type of maze has been created by Eric Solomon.  The Snakepit maze is essentially a maze on a sort of cellular automaton.  Mazes 2 and 3 are very difficult. The Searchlight maze involves mirrors. These are not very difficult, but look attractive I think.

The world's most beautiful Periodic Table Display is now at DePauw University.

Material added 10 November 2003

My third column for maa.org talks about matrix revolutions and groups.  I finally made a really nice picture of all the Archimedean points, it's near the end.  One link I eventually took out referred to Nova's The Elegant Universe, which discusses string theory.  Near the middle of the show, everything boiled down to a formula by Euler, which caused me to break out laughing (everything seems to lead back to Euler).  He also developed rotation matrices, but didn't use a matrix form.  Since I wanted to focus on matrices, I pulled the reference.

Historically, flu epidemics have a coincidental tendency to start during periods of massive solar activity.

Livio Zucca has put together a page on all (?) the equilateral pentagons that can tile the plane.

For those of you that don't have $10000 for Euler's Opera Omnia, there is now an Euler website.

Bob Abbott: The big rolling-block-maze craze is over, but maybe you'll want to mention that I just added five more of these mazes to my site. These are mazes I created for GAMES and they appeared in the magazine over the last couple of years.  They're pretty good, especially my rolling-slab maze.

The latest Games magazine is worth a look, among other things, you'll find the Games 100, a new maze by Robert Abbott, and Robert Lodge's "Ultimate Calculatrivia".

Material added 3 November 2003

My second column for maa.org concerns the Möbius Function. As a puzzle of the week, consider the numbers that are products of two different primes.  In the Möbius function, these would have value positive one. There are three distinct digits that can be arranged to make product of two distinct primes. In fact, all six arrangements give the product of two distinct primes. Can you find the smallest of these numbers? Answers and Solvers.

Erich Friedman's Math Magic discusses various Square Packings this month.

The weekly Dot-to-Dot puzzles at monkeyingaround.com are rather nice.  Walter Pullen has a page describe maze types and solving algorithms. Brian Berg is an expert at stacking cards.  Jim Morey has made a java applet that interactively connects all the Archimedean solids.

Although Euler never traveled there, he made the Bridges of Königsberg famous with the following question:  Is it possible to make a tour so that one passes just once over all the bridges over the river Preger in Königsberg?  Jan Kåhre is a mathematician that has recently visited Königsberg, and he has found a solution for the problem.

There is an audio paradox involving continually rising tones.  These are know as Shepard Tones.  You can here them at the pages of Scott Flinn, noah.org, and exploratorium.edu.

Material added 25 October 2003

I've started doing columns for maa.org.  My first one is Paterson's Worms Revisited.  Slashdot discusses it.

The NKS website, wolframscience.com, has been redesigned, and a forum has been added, along with a PDF list of open problems.  I like my Number Systems notebook for Mathematica on the Summer School portion.

The Borromean Rings, often seen in relation to a discontinued brand of beer, can be made by linking cubes together.  You should have no trouble gluing the faces of cubes together to get 3 rings that are linked in the same way as the Borromean Rings, so that they fit into a side-5 cube.  Fitting them into a side-4 cube is also possible.  Can anyone figure out how? Answer and solvers. I solved this using the Livecube system.

Stephen Collin has written a nice program for Penrose Rhombs.

Johan de Ruiter has a page of interesting Pathfinder puzzles.

Material added 18 October 2003

Various interesting contests have started.  1. Al Zimmermann regularly sponsors interesting contests.  His latest is Squares, where one must minimize the number of squares in a grid.  The top solver gets $500.  2. The 12th World Puzzle Championship has finished in Papendal, the Netherlands.  Ulrich Voigt and Wei-Hwa Huang finished 1st and 2nd.   Other information is available wpc.puzzles.com and Puzzelsport.  3. Cihan Altay: "PQRST 07 Puzzle Competition starts on October 25th Saturday at 20:00 (GMT+02). You'll have one week to solve and rate 10 puzzles." 4. Denis Borris found a way to divide a square into 8 dissimilar integer-sided right triangles.  He believes he has the smallest possible solution.  If anyone can beat his solution, he will send a $2 Canadian Toonie coin to whoever has the smallest square.  I'd also like to see the best solution for 7 dissimilar integer-sided right triangles making a square.  For this, I will send the best solution 7 different state quarters.  Send Answer. 5. The NPR puzzle of the week is numerical: 71 42 12 83 54.

Fractal Maze, by Mark J P Wolf (mark.wolf at cuw dot edu)  "Traditional mazes can always be solved by brute force methods.  Every path that is not the correct path is either a dead end or a loop of finite length, so given enough time, one can explore every path of the maze.  Fractal mazes, however, have wrong-way paths that are infinitely long, making them neither dead ends or loops; they are much harder to recognize as the wrong way.  The fractal maze is fractal because it has identical copies of itself embedded within itself, which can be entered.  In the maze below, you must enter them to solve the maze.  Begin at the MINUS and make your way to the PLUS.  When you enter a smaller copy of the maze, be sure to record the letter name of that copy, as you will have to leave this copy on the way out.  You must exit out of each nested copy of the maze that you have entered into, leaving in the reverse order that you entered them in (for example: enter A, enter B, enter C, exit C, exit B, exit A).  Think of it as a series of nested boxes.  If there is no exit path leaving the nested copy, you have reached a dead end.  The eight pins on each of the sides of the maze represent these connections to the outside of each copy (obviously, you cannot go outside of the main maze itself.  Watch your entrances and exits, and go from MINUS to PLUS. This is from a work in progress, 100 Enigmatic Puzzles.  Added: There are three different solutions to the fractal maze. 1.  The easy one, which does not go very deep, begins by entering copy C of the maze. 2. A harder solution begins by entering copy E of the maze, and goes the deepest. 3. The hardest solution, which begins by entering copy A of the maze, has the most steps." Yogy's Fractal Maze Simulator.  Answers and Solvers.  Yogy Namara's Solution.Yogy's bigger solution. Click on the image for a larger version.  Robert Abbott: "This maze embodies a mind-blowing concept!"]

George Orwell, 1984: "The Ministry of Truth -- Minitrue, in Newspeak -- was startlingly different from any other object in sight. It was an enormous pyramidal structure of glittering white concrete, soaring up, terrace after terrace, 300 metres into the air."  Did you know that North Korea built a 330 meter tall pyramid in white concrete, the Ryugyong Hotel?  It is an unfinished, unused shell, due partially to using substandard concrete. Ironically, Pyongyang contains many ministries.  A more successful pyramid is the Luxor Hotel in Las Vegas.  Now, to the puzzle:  A pyramid timer was recently built by Oskar van Deventer.  "A 3-sided Hourglass interprets binary in three phases: reset, preparation and run. In the reset phase, all sand is collected in one compartment. Next is the preparation phase, when the user has to decide several times whether to turn the Hourglass left or right. Every time, the sands distributes equally over the two lower compartment. The operation instruction shows the example where the user chooses turning right-left-right-right-left, using an 8-minute Hourglass. In this example the user ends up with 3.5 minutes of sand in the right compartment, which enables him to boil his egg in 3.5 minutes. In theory, all time intervals between 0 and 8 minutes can be achieved with this hourglass, doubling its time resolution after every turn. Question to the reader: how to use the Three-legged Hourglass to boil an egg exactly 2.25 minutes?" Answer and Solvers. Jeremy Galvagni's 3-bulb Solution. Jeremy Galvagni's tetra solution.

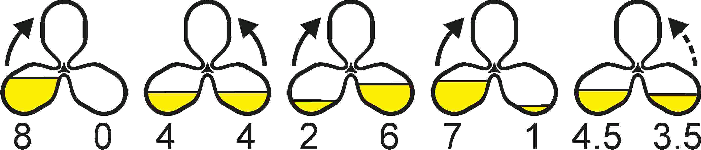
Multi-bulb hourglasses by Oskar van Deventer.  Click on the first image for greater detail.

Material added 12 October 2003

Dividing a square into smaller squares is often called the Mrs. Perkins' Quilt problem. I mentioned a while ago that Erich Friedman found a way to divide a side-67 square into 20 smaller squares all with double-digit sides. Can you find his solution?  Answer. The only solver of this puzzle was Lance Gay.  Lance followed up by finding better solutions for squares of size 88 to 90.  Robert Wainwright sent me better answers for sizes 53 and 91.  All of these new solutions were graciously accepted by Richard Guy, for the next edition of Unsolved Problems in Geometry. John Conway let me know that Dudeney named the puzzle.  Geoffrey Morley sent in transcriptions of Duijvestijn's solutions.  Erich Friedman sent me this list of best solutions (Antony Boucher and Lance Gay filled in the blanks). The current best known solutions are as follows: {1 | 1}, {4 | 2}, {6 | 3}, {7 | 4}, {8 | 5}, {9 | 6,7}, {10 | 8,9}, {11 | 10-13}, {12 | 14-17}, {13 | 18-23}, {14 | 24-29}, {15 | 30-39,41}, {16 | 40,42-53}, {17 | 54-70}, {18 | 71-91}, {19 | 92-108}.   Lance Gay:  "Since seeing your write-up on mathpuzzle.com last month, I have written some Mrs. Perkins quilt search software to look for solutions. For fun, I added a routine to print out the bitmaps of solutions. I run my searches on a pair of 1.8 GHz MS-Windows machines. It appears that computers have gotten faster since people have last done some serious searching. For now, I have completed all searching for sides up to 100. I am now concentrating on larger squares (such as attempting to beat the order-20 side-154 square). My search algorithm is not exhaustive so the trick is reducing the search space to the most fruitful areas."  John Conway: "You might add the two 1950s papers both called "Mrs Perkins's Quilt", one by me and one by G.B.Trustrum, in Proc. Camb. Phil. Soc.  I gave the answers for low n, and an upper bound of order n^(1/3) for general n, which Trustrum improved to order log(n).  Since there's an obvious logarithmic lower bound, all that remains is to find the best constant.  I don't know if there's been any progress on that problem since those two papers." Antony Boucher sent me some corrections for the list, and also sent solving code.

New quilts discovered by Lance Gay.

Jorge Rezende has put together a page on magic polyhedra.

A recent Astronomy Picture of the Day showed a hurricane next to a galaxy. Both are governed by the laws of logarithmic spirals.

Material added 7 October 2003

Last year, I had a great time with Theo Gray as he won an Ignobel Prize.  This year, there was another interesting batch of winners. Theo Gray also helped to design a little product called Mathematica, made in Champaign-Urbana.  This morning, I learned about a whole host of Nobel Prize winners that are neighbors of mine -- 1. Paul Lauterbur, Nobel Prize in Medicine, 2. Anthony J Leggett, Nobel Prize in Physics, 3. Alexei Abrikosov, Nobel Prize in Physics.  I guess I live in the genius capital of the world.  If you look at that last photo, you'll see that Alexei is a Mathematica user.  I'll try to get a copy of that cool-looking notebook from him for our Infocenter.

To heighten the odd coincidences in math, physics, and Theo, Theo sent me a link to a version of Escher's Relativity in Lego a few days ago.  A gorgeous construction, well worth a look.  Lego isn't all that great of a building material for polyforms, though.  If you would like to study polycubes, you should visit livecube.com.  A 6x6x6 brick of cleverly configurable cubes is $30.  I've been wanting to try the 25 L-pentominoes in a 5x5x5 cube for awhile, and now I can finally do it.

Previous Puzzles of the week are here.