Robert Wainwright presented this puzzle at the second Gathering for Gardner conference. He gave a solution to the order 12 Partridge Puzzle, and asked if anything smaller was solvable. He also discussed material from previous Gardner articles, including perfect squares (Mathworld Link), and optimal packings (Erich's Packing Center link). Example perfect square: pack squares with sides (1 2 3 4 5 7 8 10 12 13 14 15 16 19 21 28 29 31 32 37 38 41 44) into a square with side 110. Answer by A. J. W. Duijvestijn.
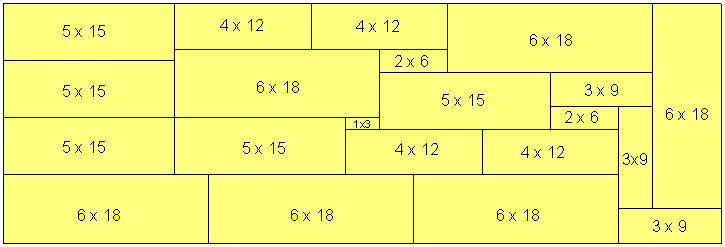
Several noted solvers (Bill Cutler, William Marshall, Michael Reid, Nob Yoshigahara) found solutions to the Partridge Puzzle. Bill proved that the order-7 Partridge problem had no solution. Bill found 2332 distinct order-8 solutions. One of them is below. The pieces are easy to make, and not too different in size. It's still very hard to solve. Can you find one of the other solutions?


| This is an interesting puzzle.
I see that part of the reason for its difficulty is that it has a parity issue. Only 9 of the 21 pieces have odd dimensions, yet the overall figure has odd dimensions. In order to fill the odd-length rows and columns, an odd number of these pieces must lie across each row and column. I expressed this concept to Erich Friedman while working on a square-packing problem of his some time ago (fewest integer-sided squares to fill a given square). I noticed that many of my best solutions for odd-sided squares (which was all of them, because composite-sided squares could invariably be done best as a blown-up version of the solution for their smallest factor) had exactly 5 odd-sided squares, and this was the minimum number of such squares by a parity argument. The area of a square of odd integer side is congruent to 1 mod 4, and the area of an even square is 0 mod 4. Thus, to fill this square, you need a number of odd squares that is 1 mod 4, and the smallest value, 1, could only be done using the degenerate solution of filling the square with a square, because of the parity issue in every row and column. The next smallest possible value was 5, and many of my solutions exhibited this, with an arrangement of odd squares that consisted of one large odd square in each of two opposite corners, and 3 smaller squares that formed an L-shaped path between those two, arranged so that each column and each row contained either 1 or 3 odd squares. In this problem, the same argument holds except that the odd pieces and overall figure now all have areas congruent to 3 mod 4. Nine is the second-smallest number of odd pieces which can fill the overall odd area, which gives us a bit more flexibility in arranging them than in the 5-odd-piece case. (But we need this flexibility, because the sizes of the shapes are constrained! In the problem I spoke of above, I could use any sized squares I wanted, though a secondary goal was to avoid repeating square sizes as much as possible. The single small 1x3 piece is a particular pain.) A critical issue here is not just getting an odd number of odd pieces on each row and each column, but also ensuring that the remaining edges after the odd pieces are all placed are all of even lengths. In the 5-odd-square cases, this was accomplished by ensuring each such edge was the sum or difference of two odd lengths. For instance, consider the solution below for the 7x7 square: aaabbcc
Here, the even edges remaining after a,d,e,h,i are inserted are all either 1+1, 3+1, or 3-1, but in particular, the lower edges of a and d are flush, making a common, even-length edge to place g against. Likewise, the upper edges of d and e are flush, making an even edge for b to lie against. (Here the lower edges of d and e are also flush, but that is not true in the general case, where e can be larger than d and h, and the area where g is in this case becomes an even-sided rectangle with a even-sided rectangular hole cut out of one corner.) Likewise, in this problem, I must ensure that edges line up appropriately
to avoid leaving behind any odd-length edges once the
Besides this, there's also a 3-parity issue that is similar; each row and column is of a multiple-of-3 length, and the long dimensions of all the pieces are multiples of 3, but the short dimensions of 12 of the pieces are not. These pieces must be paired up in that dimension somehow (presumably some going along the length of the overall shape, but some crosswise as well), and since there are an odd number of each type, it implies some interesting arrangements. /dev/joe
|
Andrew Clarke managed to solve it by hand. Here is his solution -- it's identical to Bill Cutler's solution. It's almost unique (the 15x15 square made from three 5x15 rectangles can be rotated). Note how all of Joe's parity constraints are met. The tiny 1x3 rectangle winds up being crucial to the solution. Beautiful!
William Marshall ignored an 'impossibility proof', and found an order-9 Partridge solution for equilateral triangles. The 45 triangles all fit into a triangle with side 45.
Robert Wainwright's main unsolved problem involves the order-5 set (1 2 2 3 3 3 4 4 4 4 5 5 5 5 5). Is there any rectangle or other shape that provide a solution? If you can find one, please mail it to Robert at 12 Longue Vue Avenue, New Rochelle NY 10804-4119. You may also email Robert Wainwright at rtwainwright@iname.com.
Michael Reid (packing
expert) found a type of quadrilateral of Partridge Order 4.