material added 13 December 2002

Pi has been calculated to 1.24 trillion places by Yasumasa Kanada.   John Gowland: Last term, one of my daughter's professors was bemoaning the fact that, with the advent of the calculator, people could no longer do mental arithmetic and don't even know the value of Pi. At this, my daughter told him that my parrot could quote Pi! We had intended to acquire a grey African parrot for our imminent silver wedding. However, a breeder friend asked why we were waiting. So we acquired our parrot when we had been married 22 years and 7 months. My wife said that 22/7 was Pi and he was for Us, and he became Pius, having nothing to do with the Holy Fathers of the same name! Because of his name, I taught him "Pi equals three point one four." So far so good; he says lots of other things, too. Then I thought I would try " A squared plus B squared equals C squared." Unfortunately this came out as "A squared squared equals point one four," much to my wife's delight, as she says that he must go back to math school to learn it properly! When I try to rectify it, Pius comes out with " Pi equals four. Pi equals point one four. Pi equals three point one four. What a good boy!" He does it just to upset me. Ed: John sent an "easier" puzzle, as well, which I give below:

SIMPLE ADDITION, by John Gowland.  In this crossnumber, x+y=z.  Between them, x,y, and z contain the nine digits 1 through 9.  Capitals denote entries going across, and lowercase denote down entries. Answer. Solver Commentary.

As a guest puzzle of the week, James W. Stephens has put together a very nice Christmas Tree maze at his Puzzlebeast site. He mentions to find a dog under the tree as a bonus.  This is a type of maze I haven't seen before ... thankfully, he also has some warm-up mazes available.

Jean-Charles Meyrignac ask me if I could divide to shape below along the gridlines to make a 6x6 square, in just 4 pieces. We found two different solutions.  Can you find them both?  10 Answers. Solver commentary.

Putnam questions and Putnam answers are available. Zillions-of-Games 2 is has come out.

Erich Friedman:  4, 1, 1, and 42025, 14641, 10000 are examples of triples of squares whose digits add componentwise to 666...6. Another one is 301401, 242064, 123201. Are there more?

material added 4 December 2002

Sudipta Das sent me an interesting question. Define the n-complement of a number j as the number k, such that corresponding digits of j and k always add to n.  For example, the 9-complement of 35579781903 is 64420218096.  3+6=9, 5+4=9, 5+4=9, 7+2=9, 9+0=9, and so on. Sudipta found a set of square numbers which are 6-complements.  He also found square numbers 39866596 and 82355625, that are 11-complements. He wondered if there is a third set of complementary squares. Is there?  I found a square and a cube that are 10-complements. Triangular numbers 22578-77421, 39621-60378, and 240471-759528 are all 9-complements. Find a smaller set of triangular 9-complements if you handsolve, and a longer set if you program. Answers.   Shyam Sunder Gupta has a great page about Triangular numbers.   Claudio Baiocchi wrote up a page of comments.  Luke T Pebody has proved an amazing result about the 11-complement squares 39866596 and 82355625.  If there is a higher set of square, they will be 11-complements, will have 2^k digits, and will have more than 1024 digits.

A few quick links.  Lichtenberg figures come from electrified lucite. I had a chance to show Oliver Sacks a few things when he visited our Periodic Table Table, and become a fan of hafnium. Alexey P. Stakhov has made a Museum for the Golden Ratio. But Alexey didn't know about the following math marvel.

Dave Greene: For several years I've been playing around with a couple of tilings based on recursive decomposition of the "Golden-b" tile. The tilings are three-colorable -- uniquely three-colorable, in fact (with maybe a small restriction added in one case). This is unlike three-colorings of Penrose tilings, for example, which can be three-colored in any number of ways, and so (to me) seem relatively uninteresting. One of the Golden-b tilings is an aperiodic coloring of a basically rectangular grid of tiles. The Fibonnacci sequence jumps out of it left and right; the coloring is related (a couple of layers deep) to the "Golden String" sequence: S(0) = "0", S(1) = "1", S(N) = S(N-1) & S(N-2). It's an interesting enough coloring that my wife and I have been making quilts based on it... I'm very curious as to whether anyone else has stumbled over these unique colorings, and whether there are any more general results about tilings of this kind. [Ed -- He made a great interactive page about Robert Ammann's Golden-b aperiodic tiling system, and I'm also wondering if there is a nice proof that they are 3-colorable. Here are David's Golden-b notes.  The really neat thing about this tiling is that only one shape is used, in two different sizes.]

Hexagonal Cellular Automata are a good way to generate snowflakes. At Caltech, they grow them. You've perhaps seen the photographs of Wilson "Snowflake" Bentley. My earliest mathematical memory is of folding and cutting snowflakes (the 12 repeat version. I remember, later, having a tantrum in the 3rd grade when the teacher tried to teach the class square snowflakes -- something I couldn't accept. So, she caved, and allowed anyone who wanted to make "Eddie snowflakes" (which she said with a sneer). I was the only one who went hexagonal, but I made thousands of them, for weeks, and outdid the rest of the class.) What are some non-obvious snowflake patterns in mathematics?  Write me if you have a nice one.

material added 24 November 2002

Mathematician Robert Bosch of Oberlin College has a nice algorithm for optimizing pictures with domino sets, as seen at www.dominoartwork.com.

Robert Harley found many prime factors of googleplex+1. When I wondered how he did it, Don Reble commented: "I suspect he used legendary cleverness... or should I say Legendre."

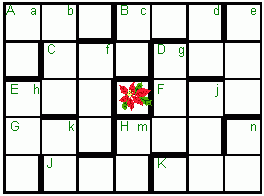
Robert Reid asked me to look at Leslie Shader's solution to his Plunk puzzle more closely -- it's quite nice. Measurements 1-20 are given by {DJ, AE, BG, BH, GH, GF, IC, EF, BF, AF, IJ, AC, EI, EG, DF, AG, BE, CJ, AB, EJ}. Can this be topped?

material added 14 November 2002

The Amazing Art site has a great collection of puzzling pictures. Deadly Rooms of Death has been released in the public domain. An explicit construction of a Universal Computer using Life has been constructed by Paul Chapman. Mark Michell has made an analysis of Hearts.  I fixed the SEARCH, above.

Paul Stephens, who offers a free bingo game, has asked which is more likely to come first in Bingo: a horizontal row, or a vertical row?   He is interested in the game theory of it, and liked my gambling odds page. Bingo is played on a 5x5 card, with B-I-N-G-O at the top to mark the columns.  B has 5 random numbers from {1,15}, I has 5 random numbers from {16,30}, N has 4 random numbers from {31,45} and a free square, G has 5 random numbers from {46,60}, O has 5 random numbers from {61,75}.  So a game might start off N32, O63, B11, B1, B3, N38, B4, G56, O75, I20, I21, N38. Analyses.

material added 4 November 2002

Nick Baxter: The third annual IPP Puzzle Design Competition starts now and continues through July, 2003. The competition was established to promote and recognize innovative new designs of mechanical puzzles. Go to the official web site for further information and summaries of past results.

Rudi Cilibrasi has added a new groove to sliding block puzzles.  Specifically, he added grooves at the bottom of squares, so that they could move only up and down or left and right.  So, how hard a puzzle can you make with that?  It turns out, very hard.  At his Orimaze site, you can see a "state tree" for an arbitrary 4x5 puzzle. He also has a javascript version of the hardest 5x5 puzzle (start with the down arrow key).  Many thanks to Wei-Hwa Huang for pointing this out to me.  Since it's so hard, I'll make it my puzzle of the week.

Isoptikon is a very nice free Geometry program offered by Paris Pamfilos of Crete.

Dan Hoey: On 21 October 2002 you posted a puzzle from Robert Reid. [Answers.]  As I understand it, it is the  n=4  case of finding a perfect collection of n Golomb rulers with  0,1,...,n-1  marks, measuring every distance from  1  to  BinomialCoefficent(n+2,3). I wrote a program that indicates the number of such ruler collections (up to reversal of the rulers) is  1,1,2,5,47,136,1  for n=0,1,2,...,6. My program ran for a few minutes for  n=5  and several days for n=6,  so I doubt I can get results for  n>6.  [Interesting, that the Reid Hexagon would be unique.  1,4,25,6,14,3 - 8,10,16,12,9 - 2,22,19,13 - 7,33,11 - 15,27 - 39]

Make a deck of 60 cards ... five colors, with 0-11 for each color. Each card is connected to the neighboring cards of its own color, cyclically (so 0 and 11 are connected). I used colors Green, Blue, Cyen, Magenta, Red. Each card is connected to a third card, off by 6 numerically, and of a different color, as given by the chart below. Thus, 9G is connected to 3M. 7C-1M, 6B-0G, 8R-2C, 2C-3C, 4M-3M are all other connections. This deck of cards makes a 60 node Cayley Graph with diameter 5, which is the largest possible.  Until Eric Weisstein pointed out the error of my ways, I thought it was the Cubic Symmetric Graph with 60 nodes and diameter 5. But they turn out to be different graphs.  I'm looking for nicer Hamiltonian cycles for both graphs, so let me know if you find one.

       GBCMR
9 1  5 MRBCG
3 7 11 RCMGB
2 6 10 CGRBM
8 0  4 BMGRC

The atom of the week is the tetraneutron. By firing Beryllium-14 atoms at a carbon target, investigators seemingly got Beryllium-10 and tetraneutrons. If Element-0 is confirmed, it will be densest of all the elements.

material added 29 October 2002

Older Material - 16 Jul 02 to 26 Aug 02

Older Material - 13 May 02 to 9 Jul 02

Older Material - 4 Mar 02 to 6 May 02

Older Material - 5 Dec 01 to 25 Feb 02