Zome

ZOME PUZZLES
by Ed Pegg Jr and George Hart The main site for Zome is here. This page is a growing collection of puzzles for it. If you would like to contribute to it, write me.

Regular Pentagon and Center
Make a regular pentagon of any size, and a node at the exact center. You may use any manner of connecting struts.

K4 (four connected nodes)
See http://www.zometool.com/manual/tetra/tetrachart.gif for a complete list.
K5 (five connected nodes)
Three B1, Three Y1, One Y2, and Three R1.
Two B1, One B2, Three Y2, Three R1, and One R2.
Three B1, One B2, Five Y1, and One R2.
Two B2, Three Y2, One Y3, One R1, Two R2, and Three R3.
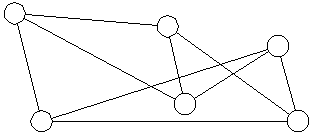
K6 (six connected nodes)
Four B1, Three B2, Six Y1, and Two R2.
Five B2, Two B3, Four Y3, and Four R1.
K7 (seven connected nodes)
Six B1, Three B2, Six Y1, and Six G1.

Overhand Knot
Two B1, Two B2, One Y1, and One R2.
Three B3, and Three Y3 (slight bending)
Three B3, and Three G2

Graph Construction (each node has three struts)

One of each: B1 B2 B3 Y1 Y2 Y3 R1 R2 R3
Two B1, Three B2, Three Y1, and One R2.
Two B2, One B3, Three Y2, One R1, and Two R2.
One B1, One B2, Two Y1, Three Y3, One R2, and One R3.
One B1, Two B2, One B3, Two Y2, One Y3, One R1, and One R2.
One B2, One B3, Two Y2, Two Y3, One R1, One R2, and One R3.

Construction Problems from http://www.georgehart.com/

In this series of puzzles, you are challenged to make six polyhedra, each having all its faces identical:
A. A tetrahedron in which every face is an isosceles triangle (but not equilateral).
B. A dodecahedron in which every face is a scalene triangle (having sides of three different lengths).
C. A polyhedron in which every face is a “kite”. (A “kite” is a convex quadrilateral in which one of the diagonals is a line of mirror symmetry.)
D. A polyhedron in which every face is a dart. (A “dart” is concave quadrilateral in which one of the diagonals is a line of mirror symmetry.) The faces have to pass through each other (like in the Kepler-Poinsot polyhedra)
E. A polyhedron in which every face is a pentagon, but not a regular pentagon.
F. A polyhedron in which every face is a trapezoid, but not a parallelogram.
Remember, in each polyhedron, all the faces are identical. Be sure your faces are planar, e.g., four vertices do not form a kite if they are not in the same plane. Also, we do not allow adjacent faces to be coplanar. For example you can’t just add the long diagonals to the kites and call that a solution to B.

Most puzzles should be RIGID structures. A figure is RIGID if every node has 3 or more struts, and every strut has 2 nodes. All of the 4 node tetrahedra in the link above are rigid.

At the page for the 34 forms of convex heptahedra, solutions have been found for the blue colored cells in the table.

I also plan to look at knots, such as the ones at http://www.cs.ubc.ca/nest/imager/contributions/scharein/cal/inlines/BackCover.jpg

My puzzle ideas are thus involved in Graph Theory and Knot Theory, primarily. Any other ideas?

I’m tempted to use Chime at http://www.mdli.com/cgi/dynamic/welcome.html, but it seems that an actual Zome program would be more interesting.