
Kites that will make 90 degree angles together.
Here's a little fact I've never fully appreciated: Pi/4 = ArcTan[y/x] + ArcTan[(x-y)/(x+y)]. If you have a 1-2 right triangle and a 1-3 right triangle, their smaller angles will sum to 45 degrees (Pi/4). 2-1 = 1, 2+1 = 3. If you make kite shapes by reflecting the 1-2 triangles and 1-3 triangles on the hypotenuses, the sharper points together will make a 90 degree angle. Other pairs of triangles also work very nicely together.

The nicest of these is the 1-2, 1-3 pair. Make a 7x7 square out of 7 dominoes, 10 1-2 kites, and 5 1-3 kites. Below you can see an 'almost' solution. It has an extra 1-3 kite, and two dominoes are missing. Here is a bigger diagram, for printing. This is a fantastic puzzle for hand solving. Try it!


Make a 7x7 square with three different shapes as indicated.
My Kites&Bricks puzzle was solved by Koshi Arai and his sons, Adrian Fisher, David Molnar, Livio Zucca, Roger Phillips, Roel Huisman, and Joseph DeVincentis. Koshi Arai found the same three solutions (1, 2, 3) that I found. Joseph found a different puzzle: Make a 7x7 square out of 8 dominoes, 12 1-2 kites, and 3 1-3 kites. I'd like to see other tricky combinations. Many of these solvers mentioned that this puzzle was particularly nice to solve. I thought so, too. Koshi Arai has made a PDF file of Kites & Bricks puzzles and solutions.
Here is a bit from Livio Zucca's page.

Last an interesting variant for PolyBiForms making: the bricks and the kites:
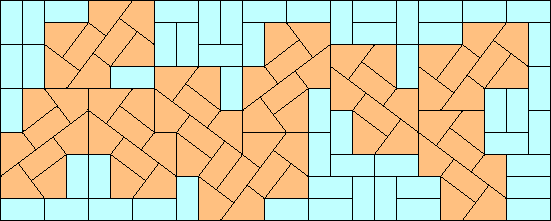
It's possible to cover a 10x10 square with 50
bricks, it's trivial. Also to insert 6 kites and 44 bricks it's easy.
28
kites and
22 bricks are less easy. Do you want to try?
Is 28 the maximum number of kites ?