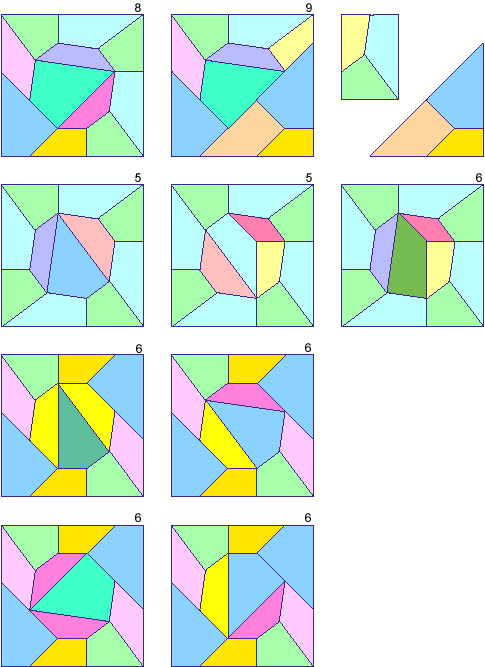
New Kites, by Ed Pegg Jr and Koshi Arai
First, take a look at the original page on Kites
and Bricks. How can these shapes be extended?
Here is the complete list of convex quadrilaterals I've looked at. The first
four numbers are the squares of the lengths. Thus, on the first one, the actual
lengths are 1, sqrt(2), sqrt(2), 1. The last four numbers are the tangents of
the angles. 1 is a 45 degree angle, qq is infinity -- a 90 degree angle. The
other angles are more irregular, but they all work with each other very nicely.
{1,2,2,1, -1,3/4,-1,4/3},
{1,1,4,4, -4/3,qq,4/3,qq},
{1,1,9,9, -3/4,qq,3/4,qq},
{1,2,1,4, -1,7,qq,4/3},
{1,2,2,9, -1,-4/3,1,4/3},
{1,2,4,9, -7,-1,3/4,qq},
{1,2,9,8, -1,7,1,-7},
{1,4,8,9, qq,-7,1,-4/3},
{1,8,2,9, -7,qq,7,qq},
{2,2,4,4, 4/3,-1,3/4,-1},
{2,2,8,8, -4/3,qq,4/3,qq},
{2,4,2,8, -1,7,qq,4/3},
{8,8,9,9, -3/4,1,-4/3,1} |
 |
The above are the pieces with only integer or sqrt[2] based sides. Parallelograms
of various sorts are also possible, as well as the trapezoids below. My next
thought is to find all the integer-only pentagons. All these shapes have either
an integer area, or an integer area + 1/2.
{1,1,4,2, qq,qq,1,-1},
{1,2,1,8, -1,-1,1,1},
{1,2,8,9, -1,qq,1,qq},
{1,2,9,2, -1,1,1,-1},
{1,4,2,9, qq,-1,1,qq},
{1,4,9,8, qq,qq,1,-1},
{2,2,4,8, qq,-1,1,qq}
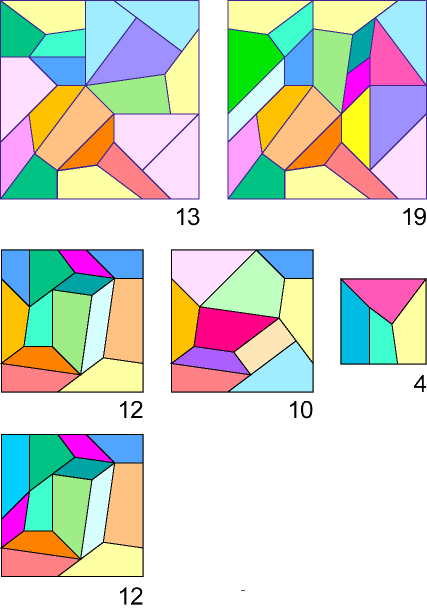
Figures by Koshi Arai
Koshi Arai -- It's not hard to make squares by selecting suitable quadrilaterals.
I think it is important to set up the restriction or condition. What restriction
would be good for making squares?? Send me
an answer.
shapes without sqrt(5) sides. Not to scale with the above.

{1,1,5,5, qq,-2,3/4,-2},
{1,1,5,9, qq,-1/2,1/2,qq},
{1,2,2,5, -1,qq,3,2},
{1,2,4,5, 1,-1,1/2,-1/2},
{1,2,5,8, 1,-1/3,1/3,-1},
{1,4,4,5, qq,qq,2,-2},
{1,5,2,8, -1/2,3,qq,1},
{1,5,4,8, 2,-2,1,-1},
{1,5,5,5, -1/2,4/3,qq,2},
{1,5,5,9, -2,qq,2,qq},
{1,5,9,5, -2,2,2,-2},
{2,2,5,5, qq,-3,4/3,-3},
{2,4,5,5, -1,2,qq,3},
{2,4,5,5, 1,-2,3/4,-1/3},
{2,4,5,9, 1,-1/2,1/2,-1},
{2,5,5,8, -3,qq,3,qq},
{2,5,8,5, -3,3,3,-3},
{2,5,8,9, 3,-3,1,-1},
{4,4,9,5, qq,qq,2,-2},
{4,5,5,8, -1/2,4/3,-3,1},
{4,5,9,8, 2,-2,1,-1},
{5,5,8,8, -4/3,3,qq,3},
{5,5,9,9, -3/4,2,qq,2}
Tossing in sqrt(10) adds the following shapes.
{1,1,8,10,qq,-1,1/2,-3},
{1,2,5,10,-1,-3,1,3},
{1,2,9,10,1,-1,1/3,-1/3},
{1,2,10,5,-1,2,1,-2},
{1,4,5,10,qq,-2,1,-3},
{1,4,10,5,qq,3,1,-1/2},
{1,5,2,10,-2,-3,2,3},
{1,5,2,10,2,-1/3,1/2,-3},
{1,5,8,10,-1/2,3,2,3},
{1,5,10,10,-2,7,4/3,-3},
{1,5,10,10,2,-7,3/4,-1/3},
{1,8,5,10,-1,3,7,3},
{1,8,5,10,1,-3,1,-1/3},
{1,9,4,10,qq,qq,3,-3},
{2,2,10,10,qq,-2,3/4,-2},
{2,4,4,10,-1,qq,3,2},
{2,4,8,10,1,-1,1/2,-1/2},
{2,5,5,10,3,-4/3,1,-2},
{2,5,9,10,-1/3,2,3,2},
{2,5,10,5,-1/3,1,7,3},
{2,8,8,10,qq,qq,2,-2},
{2,9,5,10,-1,2,-7,2},
{2,9,5,10,1,-2,1,-1/2},
{2,10,10,10,-1/2,4/3,qq,2},
{4,4,10,10,qq,-3,4/3,-3},
{4,5,5,10,-2,qq,7,3},
{4,5,5,10,2,-3/4,1,-3},
{4,5,10,5,-1/2,1,-7,2},
{4,8,10,10,-1,2,qq,3},
{4,8,10,10,1,-2,3/4,-1/3},
{5,5,8,10,3/4,-1/3,1/2,-1},
{5,5,8,10,qq,-3,2,-7},
{5,5,10,10,4/3,-1,3/4,-1},
{5,8,9,10,-1/3,1,-3,1},
{5,9,8,10,-1/2,1,-2,1},
{5,9,10,10,2,-3,4/3,-1}
Here are more pictures by Koshi Arai.