Math Games

Guilloché Patterns

Ed Pegg Jr., February 9, 2004

A guilloché pattern might be very close to you at the moment. Paper banknotes, passports, identification cards, certificates, checks, bonds, and warranties all frequently feature guilloché pattern. In figure 1, the elaborate lines are an example of such a pattern.

Figure 1. Detail from 1 Brazilian Real note.

You may have made a guilloché pattern yourself. In 1962, Denys Fisher was designing bomb detonators for NATO, and his research inspired him to invent spirograph (I frankly don't see the connection, myself). Although considered a child's toy, the spirograph has some serious math behind it. The patterns the toy produces, called epitrochoids, have been studied by Dürer, Desargues, Leibniz, Newton, L'Hospital, Bernoulli, and Euler. They belong to a class of curves called roulettes.

Figure 2. Detail from a Mexican 50 peso note.

The spirograph can be considered a wheel within a wheel, inscribing a line. That's exactly how the patterns on paper money get made, except with more wheels. When Fabergé designed his famous eggs, he used a guilloché machine. These devices are expensive, and tricky to master. The patterns they produce are almost impossible to replicate. Due to this, bank notes use guilloché patterns to deter forgeries.

Once upon a time in the United States, anyone with $50,000 could start a bank and issue banknotes. If the bank failed, these "private issue" notes became worthless. Typically, the better banks used better artists, and more elaborate guilloché patterns -- the better looking the bill, the more it was trusted. In 1863, private issue notes were abolished in favor of government currency. The elaborate guilloché patterns on the backs of these bills were printed in green, which led to the term "greenbacks."

Figure 3. Detail from a United States 1 dollar bill.

In 1877, all US currency design was handed over to the Bureau of Printing and Engraving. The guilloché machine they used, which they called a geometric lathe, is rumored to have a ten wheel system. The lines in figure 3 were made by this lathe. The machine had various settings for each wheel. The pattern generated for US currency used a series of wheel settings known only to the Sculptural Engineer that operated the lathe. For many years, that lathe was the source of all the lathe and cycloid work on US paper currency.

Today, US banknotes production is computer-assisted. Many of the design "parts" of the redesigned Series 1996 currency (the series of currency where the portraits were enlarged and moved off center) came from the lathe images in the Bureau files, assembled together on a computer. The lathe itself is in semi-retirement.

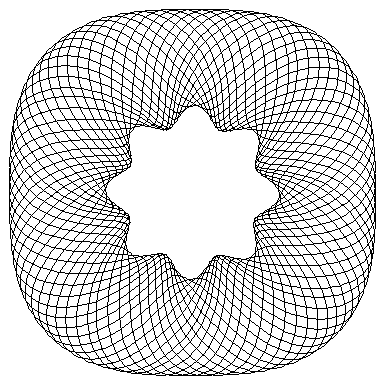
Here is an example of a computer generated guilloché. This is a three wheel pattern. Beyond that, the patterns are likely uncrackable.

Figure 4. A computer generated guilloche pattern.

Here is a detail of a banknote from Kenya. Five different types of guilloché patterns are used within a small section of the bill.

Figure 5. Detail from a Kenyan 20 shillings note.

The below image is from a Russian ruble kept by Igor Bakshee, founder of Symmetry Works, one of a handful of programs specifically creates guilloché patterns. Speaking of Russia, of all the government sites in the world, they have the best pictures of their own currency.

Figure 6. Detail from a Russian 5 rubles note.

Here is a photo of the New Zealand "Y2K" banknote -- printed on a plastic polymer. This note was produced by Securency, an Australian firm which now makes currency for 22 different nations. Y2K appears only when the clear window is folded over a different part of the note. In addition to being plastic, Australian banknotes are also toroidal, a fact noted by Martin Gardner in his book A Gardner's Workout.

Figure 7. Detail of the New Zealand 10 dollar note.

Guilloché might be a disappearing art form. I was excited to hear about the elaborate new patterns and colors employed for the new US $20 bill. Surprisingly, the new background involves a series of nested hexagons. Brazil used an identical pattern years earlier. In my opinion, the elaborately mathematical background of the Kenyan note is far better.

Figure 8. Nested hexagons, seen on the notes of both US and Brazilian currency.

These nested hexagons might be a part of another form of security. Many banknotes, it turns out, are unscannable on modern scanners. When I tried to scan the Norwegian Kroner, my computer screen turned a garish green. It turns out that the pattern of 5 circles, seen below, is a signal to scanner software to replace all colors with green and yellow. Perhaps in the future, any attempt to scan something with nested hexagons will be similarly changed. I'd rather just see microline guilloché.

Figure 9. Detail of the 200 Norwegian kroner note. Colors changed automatically by the scanning software.

References:

Mathematica Code for Figure 4:

Math Games archives.

Comments are welcome. Please send comments to Ed Pegg Jr. at ed@mathpuzzle.com.

Ed Pegg Jr. is the webmaster for mathpuzzle.com. He works at Wolfram Research, Inc. as the administrator of the Mathematica Information Center.