x -- x -- x -- x
|    |    |    |
x -- x -- x -- x
|    |    |    |
x -- x -- x -- x
     |    |
     x -- x

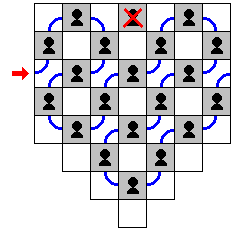
The conditions are that one edge cannot be used and one other one must
be used twice. Note that it is impossible to find a path using every
edge exactly once since there are four vertices of degree 3. All we need
to do is remove one edge and "double" another and end up with only two
vertices of odd degree. There are a few ways to do this (most, if not
all, having multiple solutions even then), such as:

20    -- 1,19 -- 2,8  -- 9
|         |       |      |
17,21 -- 4,18 -- 3,7  -- 10
|         |       |      |
16    -- 5,15 -- 6,12 -- 11
          |       |
         14   --  13

If you have to make a series of only 19 jumps (you asked for 20), then
the series of jumps is not unique but the starred square which must be
unused is unique as is the pair of starting and ending square for the
king. In that case, we are just removing an edge so we must remove the
only edge which connects two odd vertices. This is the middle edge of
the top row. There is still no unique path to jump all of the pawns,
however. One such path is:

2   --  3       14   --  13
|       |        |        |
1,5 -- 4,18 -- 15,19 -- 12,20
|       |        |        |
6   -- 7,17 -- 10,16  --  11
        |        |
        8   --   9

Dave