THE ETERNITY PUZZLE


Christopher Monckton's Eternity Puzzle (different
image, larger image), William Waite's Batman
Totem.
It's been solved by Alex Selby and Oliver Riordan.
Their Solution.
Independently, it was also solved by Guenter Stertenbrink. His
Solution.
Yahoo News
Story about winner. MSO
World story.
Do you like puzzles with big number of pieces? Try lottery, there you can make big money with few numbers.
Link to ERTL - Purchase Eternity
in United States
Link
to Hotbox (purchase Eternity in UK) The
grid for the Eternity Puzzle
My Iamond Page Polytans
at World Game Review
ISISDraw
(free, useful for drawing isomorphic grids)
Ishihama
Yoshiaki's drafter generators (at bottom of page)
The official rules
for the Eternity Puzzle
Brendan
Owen's page Mark
Pursey's page Miroslav
Vicher's page
Official
Eternity Site

Solution by Alex Selby. Eternity pieces copyright
(c) 1999 by Christopher Monckton
The MSOworld story about the Eternity puzzle is here.
It was solved by Alex Selby
and Oliver Riordan (Yahoo
story). It was also solved by Guenter Stertenbrink.

Solution by Guenter Stertenbrink.
Eternity pieces are copyright 1999 by Christopher Monckton.
Do you want to learn more about Eternity?
Join the Eternity
Mailing List. I've collected the first twenty-one digests here.
One nice study of triangles has been made by Miroslav
Vicher. His web page is here.
In particular, his research into convexity
under certain rules is worth looking at. Maybe atomic stability
and triangular convexity are related problems. No-one knows, yet.
The atomic stability problem might be easier to solve than Eternity.
The official site for Eternity is at
http://www.eternity-puzzle.co.uk/
. Eternity will soon be on sale in many more countries. So
far, the one hint I can give is that marking the grid on the pieces is
enormously helpful. It sped up my exploration of the hexadudes
by a factor of at least four. So, if you have an Eternity set, you
should mark the triangular grid on each piece, on each side.
What are the pieces? You can see them by
following the official rules: "2. No
purchase necessary to enter competition. For details and everything
needed to enter, write to Ertl Europe Ltd, FREEPOST Falcon Road, Exeter
EX2 7LB, England. This is at no cost." The pieces
have been eradicated from the web for legal / insurance reasons.
Here's a puzzle for Eternity from Patrick Hamlyn
-- Arrange 72 Eternity pieces to make 8 hexagons. Lew Baxter found
nine:
{1,3,40,62,94,101,106,168,199} {5,7,13,16,52,55,65,93,196}
{8,15,20,34,54,110,112,117,192}
{11,25,53,75,83,91,111,141,163} {12,35,44,46,89,99,119,126,131}
{18,61,82,95,103,123,133,175,207}
{19,23,31,32,33,161,167,169,202} {21,22,51,78,109,127,160,194,205}
{37,56,60,63,97,104,113,188,201}
Lew has found a total of 77 sets of 9 disjoint
9 piece hexagon tilings. There are no 10 disjoint tilings.
Ever since I read the Times article, I've
been curious. Exactly what set of pieces did Monckton use
for his puzzle? It wasn't polyominoes, polyiamonds,
or polytans.
It turned out to be a new set of pieces, which I have called polydrafters.
Each piece in the Eternity puzzle is made from twelve 30-60-90 triangles,
also known as a Drafter's Triangle (or Draughter's Triangle). It
seems that Christopher Monckton is the first person to do an exploration
of these pieces. He (CM) called the pieces polydudes
(since they are cool and not square). I've decided to follow his
naming convention for the 'sturdy polydrafters' explained below.
William Waite and Wei-Hwa
Huang (his study here)
both did explorations of polydrafters in 1998.

The 14 Tridrafters (all
75 convex shapes, larger image).
There are 6
didrafters (plus 7 rejected shapes),
14 tridrafters,
64
tetradrafters, 237 pentadrafter, 1014 hexadrafters, 4124 heptadrafters,
and 17705 octadrafters. Many thanks to Bob Harris, Joseph DeVincentis,
and Brendan Owen for calculating the higher numbers. One thing to
note in the diagram above (Miroslav Vicher) -- four pieces indicated go
'against the
grain' of the rest of the figure. If you are writing a program
to solve Eternity, keep this in mind. Miroslav Vicher has found 75
different convex figures with the tridrafters! The tridrafters
thus make an unexpectedly rich set for polyformists. The
Association of Professional Flight Attendants uses a tridrafter as
their logo.
The tridrafters make for a fairly nice set of puzzle pieces. I
had a weekly challenge to come up with figures for these pieces.
Three of the interesting figures are below.


Sawblade and Pinwheel by Bob Harris and a solvable Samarai by William
Waite.
Joe DeVincentis noticed that none of the Eternity pieces seems to have
any 30 degree vertices, or weakly hanging triangles. Christopher
Monckton eliminated these pieces to make a safer, sturdier puzzle.
I'll call these piece sturdy polydrafters.
Christopher
Monckton calls them polydudes.
Under this scheme, there 3 didrafters, 1 tridrafter, 9 tetradrafters,
15
pentadrafters, 59 hexadrafters, 152 heptadrafters,
517 octadrafters, 1547 nonadrafters, and 5064 decadrafters, 16123 hendecadrafters,
and 52630 dodecadrafters.

The 15 pentadudes (Miroslav
Vicher)
The Eternity Puzzle is rife with parity issues. We'll ignore that
for now, and instead look at the 59 Hexadudes.
Is there a convex figure they can cover? Yes, there is! Patrick
Hamlyn solved it. The pieces are colored by their parity (balanced,
plus
two, plus four,
plus
six).
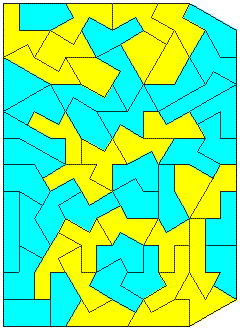


The 59 hexadudes colored by up/down parity, left/right parity, and
east/west parity.

The three parities of ETERNITY -- up/down, left/right, and east/west
For Eternity, a computer can help search for a solution. At some
point, the program may have a partial solution, but the remaining pieces
may not be able to fill the remaining area due to parity. There are
twelve ways a 30-60-90 triangle can be oriented. They can be colored
in three different ways. The balance of a piece cannot be changed
with rotations or translations.
The parity of the pieces in Eternity
|
up/down parity
|
left/right parity
|
east/west parity
|
|
balanced = 116 pieces
|
balanced = 89 pieces
|
balanced = 51 pieces
|
|
parity 2 = 90 pieces
|
parity 2 = 112 pieces
|
parity 2 = 121 pieces
|
|
parity 4 = 3 pieces
|
parity 4 = 8 pieces
|
parity 4 = 32 pieces
|
| |
|
parity 6 = 5 pieces
|
In the parity spreadsheet, all of the pieces
have a total parity of divisible by 4. Here
is why. For the octadudes, the parity distribution is: 132 (0
2 2), 100 (2 0 2), 95 (0 0 0), 87 (2 2 0), 36 (0 0 4), 34 (2 2 4), 21 (2
4 2), 17 (0 4 0), 7 (4 0 0), 7 (0 4 4), 4 (4 2 2), 3 (2 0 6), 3 (0 2 6),
and 1 (2 6 0).
Bob Harris considered the eternity parity trifecta. Any eternity
piece can be oriented so that it's E/W balance is postive (east-heavy)
and it's L/R balance is also positive (left-heavy). You can then
assign a <E/W, L/R, U/D> vector to each piece. For example, piece
1 is <2,2,-4>.
|
A: 68 are <2,2,0>
|
B: 25 are <0,0,0>
|
C: 24 are <2,0,-2>
|
D: 24 are <2,0,2>
|
E: 23 are <0,2,2>
|
|
F: 14 are <4,0,0>
|
G: 9 are <4,2,-2>
|
H: 6 are <4,2,2>
|
I: 4 are <6,2,0>
|
J: 3 are <2,4,-2>
|
|
K: 3 are <4,4,0>
|
L: 2 are <2,2,-4>
|
M: 2 are <0,4,0>
|
N: 1 is <0,0,4>
|
O: 1 is <6,0,2>
|
It turns out C and D should be combined. The above table has a
few mistakes. Here is a different enumeration
of vectors. Also, Swiss Knife Software has made a 'hardness'
list for the pieces of Eternity. I'll be adding other data as
soon as I can.
There are only four methods to affect parity. These are the four
states that any piece can be placed in, as far as its parities are concerned.
A plus (+) means the parity is unaffected, a minus (-) means the sign of
the parity is changed.
E
L U
method W: + + + (don't move, rotate 120, rotate
240)
method X: - + - (rotate 60, rotate 180, rotate
300)
method Y: + - - (flip over, flip and rotate 120,
flip and rotate 240)
method Z: - - + (flip and rotate 60, flip and
rotate 180, flip and rotate 300)
For any packing, there are essentially 60 state counts. For example,
EX is the count of pieces of class E that are placed in state X.
Following this, one obtains 17 equations with 58 unknowns with a constraint
that all unknowns are positive integers. What is the fewest number
of pieces that can be placed on the board to make a solution impossible
for parity reasons?
E/W parity equation: 2(AW-AX+AY-AZ) + 2(CW-CX+CY-CZ) + 2(DW-DX+DY-DZ)
+ ... + 6(OW-OX+OY-OZ) = 0
L/R parity equation: 2(AW+AX-AY-AZ) + 2(EW+EX-EY-EZ) + 2(GW+GX-GY-GZ)
+ ... +4(MW+MX-MY-MZ) = 0
U/D parity equation: -2(CW-CX-CY+CZ) + 2(DW-DX-DY+DZ) + 2(EW-EX-EY+EZ)
+ ... +2(OW-OX-OY+OZ) = 0
If you color the pieces by parity, they seem to group
together in a mostly filled pattern.
Ishihama Yoshiaki
has written several interactive
Java programs that generate drafters. The programs are fascinating
to watch. He's written a 12
nonadrafter hexagon, 48
nonadrafter hexagon, 36
dodecadrafter hexagon, and a
16 nonadrafter rectangle. This looks like an interesting new
type of cellular automata.
Eternity is not an easy puzzle to solve. If you play poker online you will know that there are always strategies and sequences
that lead to the winning hand. It is also important to understand the odds involved.
With poker and Eternity alike you have to see the greater picture in order to
win the game.
Who will solve the Eternity Puzzle? If you can make a nice figure
from the tridrafters, then you might be able to solve Eternity. I'm
no longer so sure that the puzzle cannot be solved by computer. The
figure below was found via computer, by Patrick M Hamlyn. I long
thought that this problem was unsolvable, but there it is.

How hard is this puzzle? I've made a little test puzzle from just
7 pieces, so that you can get an idea of your solving ability with puzzles
of this type. Arrange these 7 pieces into a
convex shape. If that's not enough, here
is a set of 7 pieces, and a set of 8 pieces. This time, I used
pieces from the set of hexadudes (sturdy hexadrafters). Rearrange
each set to form a perfect rectangle. A harder puzzle, arrange these
twelve shapes into a convex figure. Send me the answer if you
solve this last one.
Many thanks to Hotbox, Miroslav Vicher, Ishihama Yoshiaki, Brendan Owen,
Patrick M Hamlyn, Mark Parry, Joe DeVincentis, William Waite, Roger Phillips,
Bob Harris, NOBnet, David Singmaster, and Christopher Monckton for information
in this article.




