Unsolved problems
One of my favorite games is Philip Shoptaugh's Interplay.
Here's a diagram from his 1980 patent 4239230.
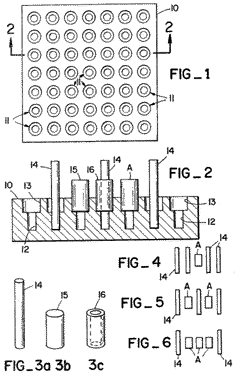Each player has 10 pegs (3a), 4 solid cylinders (3b), and 4 hollow cylinders
(3c). To win the game, you must make one of the patterns in figures
4, 5, or 6 -- a symmetrical 5 in a row of pegs and cylinders with a peg
at each end. The 5 in a row can be made vertically, horizontally,
or diagonally. A player may place a peg of his color into any opponent's
hollow cylinder already on the board. A player may place a hollow
cylinder of his color around any opponents peg already on the board.
A player may not play a peg and a hollow cylinder of the same color
in the same space.
Red has pegs on spaces 1 and 3, and a hollow cylinder at space 5.
Yes has a solid cylinder at space 4.
The above position shows how a line might be made unplayable for both sides.
Even if Red were to move his pieces, he cannot make one of the three winning
positions due to the solid cylinder. Likewise, Yellow cannot make
one of the winning positions.
Task problem: Using the full set of game pieces (Red = 10 Pegs,
4 Hollows, 4 Solids; Yellow = 10 Pegs, 4 Hollows, 4 Solids), find a position
where both sides have the other side completely locked out -- no matter
how the opponent may rearrange their pieces, a winning position is impossible.
It *is* possible, and the analysis is quite nice. Send
answer. The Solid Cylinders play a huge role, of course, but
all of the pieces seem to be needed.