
Claudio Baiocchi -- I needed a lot of time to find the enclosed solution; thus
I was very proud of it.
Simultaneous disjoint 3 cycles and 7 cycles -- very nice!
12, 36, 24, 13, 45 (to be joined with the starting 12)
14, 56, 23, 16, 25 (to be joined with the starting 14)
15, 46, 35, 26, 34 (to be joined with the starting 15)
(for the 15 problem)
Guenter Stertenbrink
For the domino-graph ,
I found 960 (0.1s) partitions into 5-cycles of adjacent disjoint dominoes
and 49152 (1.4s) partitions into 5 cycles of adjacent non-disjoint dominoes.
(complement-graph)
That graph has 72 odd holes , 150 even holes , 15 triangles ,
(each domino is member of 3 triangles)
72 odd antiholes, 105 even antiholes , 80 antitriangles ,
738015 odd rivet cycles , 725556 even rivet cycles.
(if I have no bug in the program)
I think ,it is not possible to arrange the vertices in a circle
as on Ed's page , such that the diagram is symmetric.
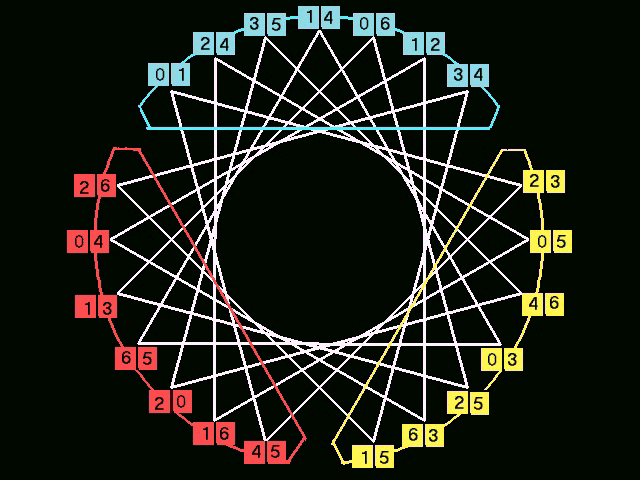
But it is possible , if we arrange the vertices on 3 circles with
same center but different radii , thus forming 3 regular pentagons.
e.g. with the 3 pentagons:
56,13,26,15,23
12,25,35,36,16
34,46,14,24,45
But e.g. the edges 56-12,56-34,12-34 will overlap in 2d and one of them is
invisible.
Dick Saunders Jr.
1/2, 3/6, 2/4, 1/5, 3/4 Circle 1
2/3, 5/6. 1/4. 3/5. 4/6 Circle 2
4/5, 1/6, 2/5, 1/3, 2/6 Circle 3
Jim Boyce
3 pair-wise disjoint 5 -cycles: This is a nice problem. I thought
about it last night while falling asleep and then this morning while
walking to the train. It didn't require pencil and paper.
1) No 5-cycle can have 3 dominos with the same number.
2) So each number appears in each 5-cycle.
3) Each 5-cycle includes 3 dominos that span all 6 numbers.
4) The other 2 dominos in the 5-cycle share numbers with 2 different
pairs of dominos.
5) The 15 dominos can be partitioned into 5 disjoint sets of 3 where
each set of 3 includes no repeated number. (These can represent the
pairings in a 5-round 6-player round-robin tournament.)
Use 3 of those 5 sets of 3 as the starts of the 3 5-cycles. Split the
other 6 into 3 pairs that do not share a number. (This can be done in 4
ways. You are looking for a matching in the complement graph of the
6-cycle.)
Each pair can extend 2 (and maybe 3) of the triples to 5-cycles. 3 of
the 4 sets of pairs include pairs that will work with any triple, so
they will clearly extend to 3 disjoint 5-cycles.
It turns out the the 4th set of pairs also works. (Each pair works with
2 triples, and it was always the same 2.) (I did use pencil and paper
to check that last sets of pairs.)
Here is something somewhat more concrete:
split into 5 triples:
1 12 36 45
2 13 42 56
3 14 53 62
4 15 64 23
5 16 25 34
split triples 4 and 5 into pairs:
each domino can go with only 1 from the other triple:
15 34 (can't work with triple 3)
64 25 (can't work with triple 2)
23 16 (can't work with triple 1)
The 4 sets of pairs are those above, or 1 of those and what remains of
triples 4 and 5 above when the pair is removed.
I'll put the pairs (in the order above) with triples 1,3,2 (in that
order) and write them in 5-cycle order:
12 34 15 36 45
14 25 64 53 62
13 42 16 13 56
-----
The 9-cycle puzzle was easy. Just write down the answer. 45 is next to
13 and 23. The other 6 dominos have either a 4 or a 5, and they
alternate so that the 4's and 5's are separated. WLOG put the 25 next
to the 13 and the14 next to the 23. The 34goes next to 25 and the 35
goes next to the 14. The 15 and 24 are left to connect the 34 and 35.
15 34 25 13 45 23 14 35 24
Your other 5-fold symmetric picture (the pentagon with interior lines
and external arcs) is one based on a tournament. Player 1 sees his
opponents in the order 65324.
You should be able to get a 7-fold symmetric picture with the blanks
added in.
Find 3 dominos that are legal near each other and that have (cyclic)
differences of 1, 2, and 3.
That is one "chunk". We ought to be able to find a cyclic permutation
of (0123456) that will give us a new "chunk" that can be next to the
first one. Keep applying that permutaion to get the next "chunks"
in
order until you are done.
This seems to work (using 0 for blank).
06 13 25
10 24 36
21 35 40
32 46 51
43 50 62
54 61 03
65 02 14
That also lists 7 circles of 3.
The last 2 columns are circles of 7. The first column would need to be
re-ordered to make the 3 circle of 7. Taking every other one seems to
work.
Now I have ridden the train home. There was more time to think about
things.
5-fold symmetry:
I played in a speed-chess tournament many years ago. It was played on a
long table. One player (designate him 1) was stationary. At the
beginning of each round, the other players moved 1 position
counter-clockwise around the table (skipping the position of player 1).
This is a simple movement that gives the pairing for a complete
round-robin tournament.
Use that movement for a 6-player tournament. Designate the other
players 2-6 in the order that they play player 1. Each game in the
tournament is mapped to a domino in an obvious way. List the dominos in
the order round1: board1, board2, board3; round2: board1, board2,
board3; ...
Adjacent domonos do not share numbers. In is obvious within a round,
because each number appears once. Since players do not play at boards 1
and 3 in adjacent rounds, it is also true at the round boundaries.
The graph has 5-fold symmetry because you go from 1 round to the next by
applying a permutation: (1) (26543).
-----
3-fold symmetry:
I want to order the dominos so that shifting them 5 positions is the
same as applying the permutation (135)(246).
First, I will just look at where to place the 1's and 2's.
-- -- -- -- --
-- -- -- -- --
-- -- -- -- --
There should be a total of 2 1's and/or 2's in each column. One column
should have the 1-2 domino.
One column should have a 1 above a 2 (cyclically); one should have a 2
above a 1; one column should have 2 1's; and one should have 2 2's.
Let's put the 1-2 in the middle column. and the one with both 1 and 2 in
the adjacent columns.
1- -- 12 -- 2-
-- 1- -- 2- --
1- 2- -- 1- 2-
There is no conflict between columns 1 and 5 because they have no
numbers in common.
Now I fill in the rest of the grid by adding 2 when I go down
(cyclically) 1 row.
13 45 12 36 24
35 16 34 25 46
15 23 56 14 26
Stephen Kloder
3 disjoint 5-cycles of P6:
12 34 56 13 46
14 25 36 15 23
35 26 45 24 16
Juha Saukkola
Here are my solutions to domino-puzzles.
Those took about 15 minutes by hand and
there are more solutions.
Juha
3*5:
12-35-14-26-34-
13-25-46-23-56-
15-36-45-16-24-
1*9:
13-24-35-14-25-34-15-23-45-
3*7:
01-23-04-15-26-34-56-
02-13-05-14-25-36-45-
03-12-06-24-16-35-46-
7*3:
01-23-45-
02-14-36-
03-16-25-
04-15-26-
05-13-46-
06-24-35-
12-34-56-
Patrick Hamlyn
My program tells me there are 155328 15-cycles using the fifteen dominos
(not counting reverses).
I set my cycles program counting 21-cycles using dominos with blanks but no
doubles. I estimate it will finish in about 100 years.
Counting three 7s and seven 3s is a bit easier.
There are 332739 distinct set of seven dominos which can form a 7-cycle,
and there are approximately a billion ways of choosing three of these at a
time so they are disjoint. The search should finish in a day or two.
There are 210 distinct set of three dominos which can form a 3-cycle, and
there are 4160 ways of choosing seven of these at a time so they are
disjoint.
Note that many of the sets of three or seven pieces can form more than one
cycle.
Here is a C program for finding 9 cycles.
Timothy Firman
Well, I found a solution to the 3 5-circles of dominoes fairly easily.
I just placed dominoes until the last two were unplacable, then did a
pairwise exchange with one of the previously placed ones for a
placable domino. No deep analysis involved.
Perhaps I was lucky...
Here's my solution for the 3 5-circles:
12 14 15
56 46 36 35 23 34
13 25 24 16 45 26
A nine-circle:
34
15 25
32 41
45 35
31 42
Michael J D Dufour
Assuming I understood the question correctly.
Clockwise with start domino repeated at end
6-5 3-2 5-1 6-2 4-3
6-4 3-1 5-2 4-1 5-3
6-1 5-4 2-1 6-3 4-2
David Yamanishi
On last week's puzzles, which I did after this week's puzzles (see previous
message), I think all of the problems are doable (3 circles of 7, 7 circles
of 3, and the circle of 21).
Following the same abstract method as in my previous note, for the 7
circles of 3 problem, there are 42 numbers total and 6 in each small
circle. There are seven numbers total, so we have to not use one for each
of the small circles. To use the numbers up evenly (there are 6 of each),
we must cycle the unused one through the sequence.
So, again using letters to denote distinct numbers, one possible set of
orderings is:
ab, ce, dg (pick so that the first is adjacent, the second has one between,
the third two between, so that when the numbers are cycled, none of the
dominoes will recur)
Now, to assign numbers for the six circles (* represents a blank):
a * 1 2 3 4 5 6
b 1 2 3 4 5 6 *
c 2 3 4 5 6 * 1
d 3 4 5 6 * 1 2
e 4 5 6 * 1 2 3
f 5 6 * 1 2 3 4
g 6 * 1 2 3 4 5
The answer based on these numbers would be:
*1, 24, 36
12, 35, *4
23, 46, 15
34, *5, 26
45, 16, *3
56, *2, 14
*6, 13, 25
Any initial sequential ordering will do, then cycle it mechanically.
For the 7 circles of 3 problem, there are again 42 numbers, now divided
into circles with 14 numbers each. Since there are six of each number, the
easy way to do it is to use up two of each number per circle.
One such set of sequences would be:
ae, bf, cg, ad, be, cf, dg (generated basically by spreading out each pair
of numbers as much as possible)
ab, cd, ef, ag, bc, de, fg (generated by substituting the letters acegbdf
for the letters abcdefg above -- the new sequence skips every other letter)
af, bd, eg, ac, df, bg, ce (generated by substituting the letters adgcfbe
for the letters abcdefg above -- the new sequence skips pairs of letters)
Assigning the numbers
a *
b 1
c 2
d 3
e 4
f 5
g 6
yields an answer of:
*4, 15, 26, *3, 14, 25, 36
*1, 23, 45, *6, 12, 34, 56
*5, 13, 46, *2, 35, 16, 24
Again, any sequential ordering will work.
For the circle of 21, I again used letters because they're easier for me to
handle, for some reason. I spread out the a's as much as possible:
ab, **, **, ac, **, **, ad, **, **, ae, **, **, af, **, **, ag, **, **, **,
**, **
Now, borrowing the letter sequence from the 3 circles of 5 from this week's
puzzle (ab, ce, ad, bc, df), substituting e for f so that the numbers are
used evenly (ab, ce, ad, bc, de), and substituting bcdef for abcde (since a
is used up), we get
bc, df, be, cd, ef
which I'll use to fill up the five gaps at the end, with the bc first so it
doesn't adjoin the ab at the beginning.
ab, **, **, ac, **, **, ad, **, **, ae, **, **, af, **, **, ag, bc, df, be,
cd, ef
This leaves ten dominoes:
bd, bf, bg, ce, cg, cg, de, dg, eg, fg
to be arranged into five pairs.
There are five g's, so the pairs will each have one of those dominoes and
one other. There are lots and lots of ways to match them up (3 or 4
possible matches for each), but one way is:
bd, cg
bf, eg
bg, ce
cg, dg
de, fg
Squeezing these by trial and error into the five pair-sized gaps above, one
possible sequence overall is:
ab, de, fg, ac, bf, eg, ad, ce, bg, ae, cf, dg, af, cg, bd, ag, bc, df, be,
cd, ef
I not sure whether other combinations of the pairs matched up might have
worked, this may have been fortuitous.
Assigning numbers:
a *
b 1
c 2
d 3
e 4
f 5
g 6
We get:
*1, 34, 56, *2, 15, 46, *3, 24, 16, *4, 25, 36, *5, 26, 13, *6, 12, 35, 14,
23, 45
Again, any sequential ordering assigned to the letters will do.
Can you tell I don't like elegant solutions? :)
On the circle of nine, I got:
13, 24, 35, 14, 25, 34, 15, 23, 45
Spreading out the dominoes with a one, that leaves six dominoes, which
necessarily fall into three pairs, which can each fit only one way between
the ones.
On the three circles of five, the answer is yes. For example:
12, 35, 14, 23, 46
56, 13, 25, 16, 24
34, 15, 36, 45, 26
There are 30 numbers total, 5 each of 1 through 6. Three circles would have
ten numbers each. To use them up evenly, each circle should have two each
of four numbers and one each of two numbers, cycling the two numbers with
one each through the range. Abstracting from the numbers, one possible
arrangement is:
ab, ce, ad, bc, df; where the letters denote distinct numbers
Assigning the numbers as follows:
a 1 5 3
b 2 6 4
c 3 1 5
d 4 2 6
e 5 3 1
f 6 4 2
produces the answer above. The numbers could be assigned in any sequential
order, and cycled through mechanically.
Nice puzzle!
Joseph DeVincentis
You have four each of the numbers 3, 4, and 5 here (for a total
of 12 instances of these numbers), in a circle of 9 dominoes, so
you must have three overlaps (and there will be exactly three:
the 3-4, 4-5, and 3-5 dominoes) and no dominoes that lack any
of these numbers (which we have). The other dominoes must be
arranged in a strict pattern around those three; for each number
in (3, 4, 5) must be in every other position in a 7-domino arc
of the circle, with two adjacent dominoes without this number
appearing only once around the circle.
So I start by placing the 3-5. The dominoes on either side must both
have a 4, since neither can have a 3 or 5:
4-? 3-5 4-?
The next dominoes on either end of the chain must be one with a 3 and
one with a 5. Beyond the one with a 3 is one with a 5, and beyond the
one with a 5 is one with a 3. We don't have another 3-5, and each number
can only have one pair of dominoes without it, so we must have two
dominoes without a 3 one one side of the 3-5 (followed by a domino with
a 3) and two dominoes without a 5 on the other side of the 3-5 (followed
by a domino with a 5.
5-? 3-? 4-? 3-5 4-? 5-? 3-?
Note that the 3-4 and 4-5 cannot be any of the first two dominoes on
either side of the 3-5. The ones adjacent to the 3-5 cannot have
a 3 or 5, but must have a 4, and the next ones away from the 3-5
cannot have a 4. The same is true for the other combinations of
3, 4, 5 around the 4-5 and 3-4 dominoes. Thus, the 3-4, 4-5, and 3-5
must appear in every third position around the circle.
By filling in the analogous relationships around the 3-4 and the 4-5,
we get everything but the positions of the 1s and 2s:
... 3-? 5-4 3-? 4-? 3-5 4-? 5-? 3-4 5-? ...
Specifying any 1 or 2 forces the other on the domino adjacent to it
and the other on the other domino in the circle written with the same
symbols above (that is, specifying the 4-2 forces the 4-1 elsewhere on
the circle, as well as the 3-1 or 5-1 adjacent to it). Those numbers
force other 1s and 2s, such that there are just two solutions that
involve swapping all the 1s and 2s.
... 3-1 5-4 3-2 4-1 3-5 4-2 5-1 3-4 5-2 ...
... 3-2 5-4 3-1 4-2 3-5 4-1 5-2 3-4 5-1 ...
I found a solution for three disjoint 5-cycles in the graph of the
15 non-double dominoes that have only 1, 2, 3, 4, 5, 6.
1-5 2-4 6-3 5-4 2-3
1-4 6-2 3-4 1-2 5-6
3-5 1-6 5-2 3-1 4-6
(These were formed from the 2nd diagram of this graph, after finding a
way to make a cycle of 5 using 5 of the 6 dominoes in two of the small
groups, then finding a way to choose these so that remaining dominoes
make a cycle.)
Three circles of seven dominoes adding blanks to the above:
0-1 2-3 4-5 6-0 1-2 3-4 5-6
0-2 4-6 1-3 5-0 2-4 6-1 3-5
0-3 6-2 5-1 4-0 3-6 2-5 1-4
(I think the patterns here are pretty obvious. I sorted the dominoes
into three symmetric groups, 0-1 1-2 2-3 etc., so that each group
contained each number twice, and each pair of adjacent dominoes DID
contain a like number, then took every second domino from these groups,
and got the above.)
Since each group of three consecutive dominoes in the above sets contains
6 unique numbers, to make 7 circles of 3, choose one domino from each
cycle such that none share numbers, then the remaining strings of 6
split into two valid sets of 3, each.
3-4 6-1 2-5
5-6 0-1 2-3 4-5 6-0 1-2
3-5 0-2 4-6 1-3 5-0 2-4
1-4 0-3 6-2 5-1 4-0 3-6
Matt Elder
circle of 9:
34 - 25 - 14 - 35 - 24 - 13 - 45 - 23 - 15.
3 circles of 5:
12 - 34 - 15 - 26 - 35
13 - 46 - 25 - 14 - 56
23 - 45 - 36 - 24 - 16