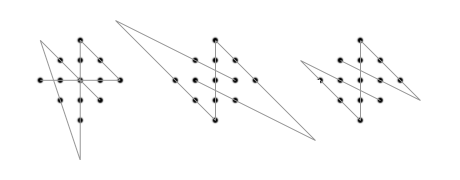
Serhiy's Constellation puzzle was solved by Ali Muñiz, Brian Pomfret,
Nick Baxter,
Igor Krivokon, Jens-Christian Larsen, mike kurtinitis, Brian Kwoh-Gain,
and all the people below.

Jean-Charles Meyrignac has placed answers to this and related problems at euler.free.fr.
My own page http://www.mathpuzzle.com/dots.html is related, too.
----------------------------------------------------
Hi Ed,
Are you desparate for solvers? Your site counter is over 720,000 so you shouldn't
be!
Maybe most are like me: I don't bother to do or send in answers to easy or standard
problems!
Okay, attached is the answer to the 13-stars problem. Very straightforward problem
--- it practically screams symmetry!
Bob Kraus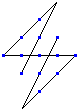
------------------------------------------
I was puzzled ...
... for quite a while, then I used a 2D CAD program to draw lines freely until I finally saw the light!
http://www.joebecker.net/constellation.gif
Thank you great gentlemen for your puzzling efforts in the past year, have a
Happy and Puzzling New Year!!
Joe
-----------------------------------------------------------------------
Since you reposted Serhiy Grabarchuk's Constellation puzzle, I thought
I'd give it a try even though it has nothing to do with sorting...
Here's a solution attached as a gif image.
- Ron Zeno
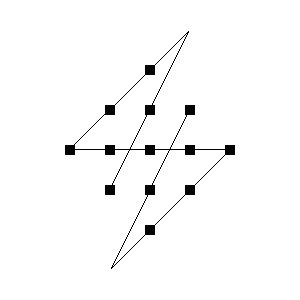
-------------------------------------------------------------------
Either I solved this puzzle in 10 seconds, or I don't
understand the instructions.
Here's a crude ASCII diagram of my solution. Two of
my lines extend outside of the constellation. The
fourth line is straight, but since it's not at 45 degrees,
it appears broken on my diagram.
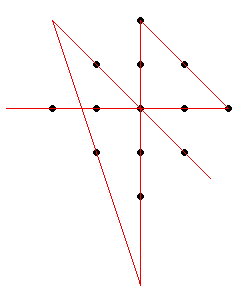
A less obvious solution: draw vertical lines through
each line of (1, 3, 5, 3, 1) stars, extending to the
top of the card. Then, roll the card into a cone such
that the lines meet at its vertex.
-Dan Hennessy
-----------------------------------------------------
Label each star with a letter as in the following:
..A
.BCD
EFGHI
.JKL
..M
Extend the lines EBA and JC toward the upper right until they intersect at
a
point we'll call X. Extend the lines ILM and DK toward the lower left until
they intersect at a point we'll call Y.
The solution is the comprised of the following connected line segments:
JX (passes through C),
XE (passes through A and B),
EI (passes through F, G and H),
IY (passes through L and M), and
YD (passes through K)
If instead you extend JC toward the lower left to intersect with ILM at Y'
and extend DK toward the upper right to intersect with EBA at X' you can
construct a similar answer (KX', X'E, EI, IY', Y'C), but the total line
length will be greater.
Each of the above solutions can be rotated and reflected four different ways
for a total of 8 solutions.
Jim Reed
-------------------------------------------------------------------------
Howdy, Ed,
Here's my solution (attached .gif, and ascii drawing below). I solved it
when I first saw it several days ago, but I'm not the type that ends up
sending in solutions very often. I had a harder time solving it today; my
memory must be going.
-- -- Bob Harris

----------------------------------------------------------------
Ed,
This puzzle was harder than it looked.
I finally solved it.
To give my solution, lay the puzzle on a coordinate plane, centered on the origin
(The top star is at (0,2) the bottom is at (0,-2), etc.
The endpoints of the connected segments are (0,-2), (0,2), (2,0), (-3,0), (3,-3),
(-1,1).
Notice the segments reach beyond the boundaries of the figure. This is generally
the key to this type of puzzle.
The next questions are: can this be solved with no star contained in more than
one segement?
I don't think it can with 5.
-Jeremy Galvagni
--------------------------------------------------------------------
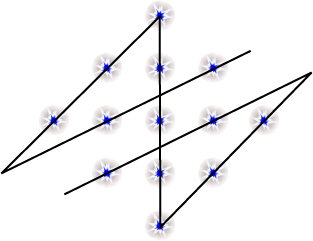
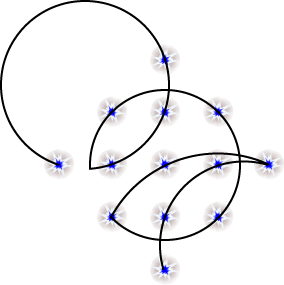
Hi Ed,
I wish you a Happy New Year!
I was spending busy days, but now I have a short holiday of new year.
It's good for taking a rest. How was your new year's day? I helped my
father because his house is the shrine (What!) and many people come to
pray for a new year. It's a first annual event.
The attached file is the answer of the constellation puzzle. the other
one is the case of it useing connected arc instead of straight line.
Eric Iverson's year are ..., 1421, 2000, 2002, 2013, 2020, ...
-- Koshi Arai
-----------------------------------------------
Hi Ed,
Here's my answer to the Constellation puzzle. I expect lots of people
managed it but didn't bother sending it to you. Anyway, it was
enjoyable. Amazing that such a simple puzzle is new. You'd have thought
H E Dudeney or Sam Lloyd would have done it.
Regards
Chris Lusby Taylor
------------------------------------------------
I wrote a program to solve this puzzle, and found the 18 following
solutions (I didn't remove rotations/symmetries).
(0,0) (6,6) (0,3) (5,3) (3,1) (3,5)
(0,0) (6,6) (0,3) (5,3) (3,1) (3,6)
(0,0) (6,6) (3,0) (3,5) (1,3) (5,3)
(0,0) (6,6) (3,0) (3,5) (1,3) (6,3)
(0,1) (6,4) (3,1) (3,5) (0,2) (4,4)
(0,1) (6,4) (3,1) (3,5) (0,2) (6,5)
(0,3) (5,3) (3,1) (3,6) (0,0) (4,4)
(0,3) (5,3) (3,1) (3,6) (0,0) (5,5)
(0,3) (5,3) (3,1) (3,6) (0,0) (6,6)
(0,3) (5,3) (3,5) (3,0) (0,6) (4,2)
(0,3) (5,3) (3,5) (3,0) (0,6) (5,1)
(0,3) (5,3) (3,5) (3,0) (0,6) (6,0)
(0,5) (6,2) (3,5) (3,1) (0,4) (4,2)
(0,5) (6,2) (3,5) (3,1) (0,4) (6,1)
(0,6) (6,0) (0,3) (5,3) (3,5) (3,0)
(0,6) (6,0) (0,3) (5,3) (3,5) (3,1)
(0,6) (6,0) (3,6) (3,1) (1,3) (5,3)
(0,6) (6,0) (3,6) (3,1) (1,3) (6,3)
Notation: number the rows and colums of a 7*7 board with 0 to 6.
These are the coordinates of all the points.
Jean-Charles Meyrignac
-----------------------------------------------------------------------
I solved the constellation puzzle in the shower a week ago (looking at the
tiling helped the visualization), but I supposed that lots of people had
solved it, so I didn't send in the answer.
If the set of points is { (x,y) | |x|+|y|=<2} then my solution has the
property that it also passes through the points (1,3) and (-1,-3).
The 5 line segments are (-1,-1) to (1,3) to (-2,0) to (2,0) to (-1,-3) to
(1,1).
Very sweet.
Cheers,
Andrew Buchanan.
--------------------------------------------------------------------
If we put origin into centre of constellation then solution looks like:
>
>(-1,0)->(5,-3)->(0,2)->(0,-2)->(-5,3)->(1,0)
>
>1-st segment will cross stars (-1,0) and (1,-1)
>2-nd segment will cross stars (2,0), (1,1) and (0,2)
>3-rd segment will cross stars (0,2), (0,1), (0,0), (0,-1) and (0,-2)
>4-th segment will cross stars (0,-2), (-1,-1) and (-2,0)
>5-th segment will cross stars (-1,1) and (1,0)
>
I found that this is not the only solution. There is one more (and more compact
than the first one)
(-1,1)->(3,-1)->(0,2)->(0,-2)->(-3,1)->(1,-1)
1-st segment will cross stars (-1,1) and (1,0)
2-nd segment will cross stars (2,0), (1,1) and (0,2)
3-rd segment will cross stars (0,2), (0,1), (0,0), (0,-1) and (0,-2)
4-th segment will cross stars (0,-2), (-1,-1) and (-2,0)
5-th segment will cross stars (-1,0) and (1,-1)
Alexey Vorobyov
---------------------------------------------------------------------
Start at
the top star, go down to the bottom star, diagonal up to the left-most star,
straight across to one position past the right-most star, up and left at a
knight's-move diagonal for 3 knight's moves, passing through the last star
on the upper right edge of the figure, and finally a diagonal down through
the remaining two stars.
Joseph DeVincentis
--------------------------------------------------------------------