A cake with a corner missing can be cut into 7 unequally sized pieces with 3 cuts, following the gridlines. None of the cuts cross themselves, and each crosses the other cuts exactly once. Following these rules, cut the cake into 7 equally sized pieces with 3 cuts. Send answer. Can any find an equality 4-cut, with 11 pieces?

ANSWERS

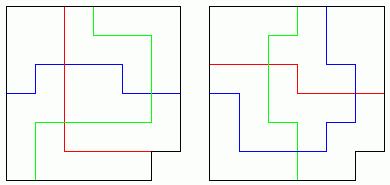
There are two solutions to the puzzle. Will Shortz sent a comment: "Beautiful puzzle. I've never seen anything like this before."

Sending Solution #1 were

Nikolov Daniel: I'm sending you my solution of the puzzle!
Bryce Herdt
Warren Phillips (who also solved a 4 cut cake)
Aad van de Wetering
Chris Lusby Taylor (who also solved a 4 cut cake)

Sending Solution #2 were

Emmanuel Seynaeve
Joseph DeVincentis

Serhiy Grabarchuk sent in both solutions. "Attached is my solution to a cute Cake Cutting puzzle. It seems this puzzle has more than one solutions."

Chris Lusby Taylor also found both solutions. "Happy New Year from England.

Pretty easy puzzle this. Took all of two minutes to find the first solution, another 15 to find the second and half an hour or so to prove, informally, that there are no others. My method was to regard the cake as a central pentomino surrounded by 6 pentominos. The cuts separating those 6 must meet only at corners of the central pentomino. For central pentominos other than the P and F pentominoes I couldn't find any way this could be done with equal sized, er, pentominos.

Best wishes and many thanks for a most entertaining column."