

ANSWERS
Claudio Baiocchi
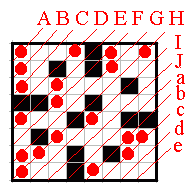
Black squares do not disconnect the board; thus in all
the squares of a same diagonal must appear the same
digit. With the notations of the picture
below the null digit could be only in diagonals
J, a, d and e; but values in A and a (as well as in
B and b, C and c, ...) must coincide; thus the value
0 must be in diagonal J.
Matthew Prins
Given that each number must have its digits in consecutive
increasing order, with 0 being allowed to follow 9, any
solution to the puzzle must be in this form:
[x+1] [x+2] [x+3] [x+4] OOO00
[x+6] [x+7] [x+8]
[x+2] [x+3] 00000 [x+5] OOO00 [x+7] [x+8] [x+9]
[x+3] [x+4] [x+5] [x+6] [x+7] [x+8] 00000 [x]
00000 00000 [x+6] [x+7] OOO00 [x+9] [x] [x+1]
[x+5] [x+6] [x+7] [x+8] [x+9] [x] 00000 00000
[x+6] 00000 [x+8] [x+9] [x] [x+1] [x+2] [x+3]
[x+7] [x+8] [x+9] OOO00 [x+1] 00000 [x+3] [x+4]
[x+8] [x+9] [x] OOO00 [x+2] [x+3] [x+4] [x+5]
where x is an integer between
0 and 9 inclusive,
and where [a] = the last digit of a.
Since no number is allowed to start with the digit 0, and
because all the digits going across the top of the puzzle
or the left side of the puzzle start a number, we know
that:
[x+1] <> 0 and
[x+2] <> 0 and
[x+3] <> 0 and
[x+5] <> 0 and
[x+5] <> 0 and
[x+6] <> 0 and
[x+7] <> 0 and
[x+8] <> 0.
Therefore,
x <> 9 and
x <> 8 and
x <> 7 and
x <> 6 and
x <> 5 and
x <> 4 and
x <> 3 and
x <> 2.
Thus, x can only be 0 or 1.
If x=0, then the puzzle is
1234 678
23 5 789
345678 0
67 901
567 90
6 890123
789 1 34
890 2345
which is a legitimate solution to the puzzle.
If x=1, then the puzzle is
2345 789
34 6 890
456789 1
78 012
678 01
7 901234
890 2 45
901 3456
which is not a legitimate
solution to the puzzle, because
the numbers 01 and 012 appear, which do not follow the
rules of the game.
Erwin Eichner
either I didn't get the point or the puzzle deserves his name.
1234X678
23X5X789
345678X0
XX67X901
567X90XX
6X890123
789X1X34
890X2345
With numbers increasing from left to right and from up to down (like in a
cross-word-puzzle), it is the only way to get it.
........
.abcdef.
.bcdefg.
.cdefgh.
.defghi.
........and so on,
You could start with any digit in the left upper corner, but with every other
digit exept 1, there would be numbers beginning with 0, witch is not allowed.
With changing digits in the
left upper corner, the line of "0" will move like
........ in the direction \....... upwards, beeing on every occasion exept
........ .\......
.......0 ..\.....
......0. ...\....
.....0.. ....\...
....0... .....\..
...0.... ......\.
..0..... .......\
the solution on the beginning of a number.
Andy Latto
1234x678
23x5x789
345678x0
xx67x901
567x90xx
6x890123
789x1x34
890x2345
Any other solution would have
to add the same number to each
digit (mod 10); since numbers start with every digit from 1 to 9,
any such addition would start some number with a 0.
Dave Tuller
A pretty easy puzzle. The unique solution is forced by placing a 1 in
the upper left corner. If the upper left corner has the digit x, then
the diagonals parallel to the main diagonal from the lower left to the
upper right all have the same digit in it. Counting the upper left
corner as the first diagonal, the only one of the first ten diagonals
that doesn't contain a square which starts an entry is the tenth one.
Since all ten digits must be represented in those ten consecutive
diagonals, the tenth diagonal must contain all zeroes. Therefore the
upper left corner has a 1.
Brendan Owen
I liked the puzzle by Bob Kraus.
_ _ _ _ _ _ _ _
|_|_|_|_|#|_|_|_|
|_|_|#|_|#|_|_|_|
|_|_|_|_|_|_|#|_|
|#|#|_|_|#|_|_|_|
|_|_|_|#|_|_|#|#|
|_|#|_|_|_|_|_|_|
|_|_|_|#|_|#|_|_|
|_|_|_|#|_|_|_|_|
A number may not begin with
a zero, so mark all the squares which
cannot be a zero. This is true of all the squares which have an edge or
# to the left or above and not to the right or below respectively.
_ _ _ _ _ _ _ _
|X|X|_|X|#|X|X|X|
|X|_|#|_|#|X|_|_|
|X|_|X|_|_|_|#|_|
|#|#|_|_|#|X|_|_|
|X|_|_|#|X|_|#|#|
|_|#|X|_|_|_|X|X|
|X|X|_|#|_|#|X|_|
|X|_|_|#|X|_|_|_|
All the digits are in consecutive increasing order therefore the digits
along the / diagonal are all the same. Therefore a square cannot be a
zero if anywhere along the / diagonal cannot be a zero.
_ _ _ _ _ _ _ _
|X|X|X|X|#|X|X|X|
|X|X|#|X|#|X|X|X|
|X|X|X|X|X|X|#|_|
|#|#|X|X|#|X|_|_|
|X|X|X|#|X|_|#|#|
|X|#|X|X|_|_|X|X|
|X|X|X|#|_|#|X|_|
|X|X|_|#|X|X|_|_|
The last three 'valid' / diagonals
cannot be zero either because if you
count back 10 / diagonals you will find that / diagonal cannot be zero.
_ _ _ _ _ _ _ _
|X|X|X|X|#|X|X|X|
|X|X|#|X|#|X|X|X|
|X|X|X|X|X|X|#|_|
|#|#|X|X|#|X|_|X|
|X|X|X|#|X|_|#|#|
|X|#|X|X|_|X|X|X|
|X|X|X|#|X|#|X|X|
|X|X|_|#|X|X|X|X|
Placing the other digits gives
you the only solution.
John Gowland
Yes, I was Fooled.
I left it for a couple of
days before I applied my mind to it. I looked at
random parts of the puzzle before starting in earnest with a 1 in the first
square - and of course it solved itself!
You have 8s in the long diagonal.
Anything else and you have to start a
number with zero.
Thank you!
Lance Nathan
Very cute puzzle! I did it the mindless way, setting up a spreadsheet
with each number being mod(x+1,10) where x is the cell above or to the
left of it. Then I put 0 in the upper left and noted which digit didn't
start a number, and only 9 didn't; therefore, the number in the upper left
needed to be 1.
Afterwards, I noticed that--of
course!--the left-up-to-the-right diagonals
(i.e. / ) were all the same digit; one had only to check which of the
first ten diagonals contained no squares which started a number, and fill
'0' into those squares.
Is that what made it an April
Fools puzzle--that there was such an easy
way to bypass the brute force method?
Chris Lusby Taylor
Looks pretty simple. The digits in each / diagonal are the same. If any
square in a diagonal starts a number, that diagonal's digit may not be
0. Every ten diagonals, the digits repeat. There are five / diagonals in
which none of the squares start a number, but only one which isn't ten
away from a diagonal with a starting square.
This diagonal must therefore have the zeros, making the top left square
a one.
But, as it's April Fool's Day, maybe I'm making a fool of myself.
Keep up the good work.
Craig Ivey
I have attached the solution to the April 1 puzzle. I can't explain in
mathematical terms why it has a unique solution. It just does. :-)

Dick Saunders Jr.
The entire puzzle will be filled by placing first integer.
Fill in the puzzle as if there were no blanks.
You can see that the zeros arrange themselves diagonally.
Top left corner can be only 1,2,or 7. Else left vertical row will begin with
a zero.
Diagonal row of zeros rule out 1,2.
Seven is it!!
Stephen Kloder
Clearly, the numbers along any top-right to bottom-left diagonal will
have the same value. Therefore it is simply a matter of finding a
diagonal (or diagonal pair) that does not cross the beginning of a
multiple-digit row or column. There is only one such diagonal (hence
the solution's uniqueness), and the 0s are placed there:
1234X678
23X5X789
345678X0
XX67X901
567X90XX
6X890423
789X1X34
890X2345
Alex Fink.
The solution to the April Fool Puzzle is
1234.678
23.5.789
345678.0
..67.901
567.90..
6.890123
789.1.34
890.2345
To construct this solution,
we start by placing an arbitrary digit
somewhere in the grid (say a zero in the upper-left corner):
0 .
. .
.
.. .
. ..
.
. .
.
Then, because each digit has
to be one more than those above and to its
left, the grid can be filled with ease:
0123.567
12.4.678
234567.9
..56.890
456.89..
5.789012
678.0.23
789.1234
At this point the first digits
of each number are 0, 5, 1, 6, 2, 5, 8,
4, 8, 7, 6, 2, 7, 1 (for across numbers), 0, 4, 1, 7, 4, 3, 8, 5, 6, 1,
7, 2 (for down numbers). Since no number can start with zero, a digit
that is not in this list must represent zero. The only such digit is 9,
therefore the 9s in the grid above represent zeros and the unique
solution can be filled in as above.
Juan Montalvo Bressi
It's really obvious that the upper-left square is a 1, then you can fill the
board.
You can fill the n=1 to 8 rows beginin with "n" and adding one per
column. n+10=n. You will notice that n+9 is the only value that doesn't begin
any number. So n+9=0. n+9+1=n+10=n=1, etc.
Richard Fitzgerald
All diagonals running from top right to bottom left will have the
same number. Since no multidigit number can begin with 0, there's
only one possible diagonal that can be 0:
Matt L. Jones
If you don't count 1-digit entries, then the solution is:
1234*678
23*5*789
345678*0
**67*901
567*90**
6*890123
789*1*34
890*2345
The 0 diagonal in this grid
is the only one that does not allow 0 to start a
number. Put the 0s in the 1, 4 and 5 diagonals below that, and you'd have to
have another row of 0s (where the upper 1, 4, and 5 diagonals are,
respectively).
However, you said nothing
about hexadecimals!!! Yes, 0 is _allowed_ to follow
9, but that doesn't mean it _must_ follow 9. :-P If you use those
stipulations, then there are a few solutions (otherwise, 0 must follow F, and
the 0 rows would go where they were noted in the above grid). That is, of
course, unless you're still allowing 1-digit numbers to count.
1234*678
23*5*789
345678*A
**67*9AB
567*9A**
6*89ABCD
789*B*DE
89A*CDEF
James Lewis Melby
This works only if the rules are clarified to state that "0" by itself
is a valid number, but that "01" or "01234", etc. are not
valid. This answer is unique because if every number is composed of consecutive
increasing digits, all digits can be determined from the first digit placed
in the framework. Therefore there are only ten possible configurations. Nine
of which contain numbers begining with "01...".
Andrew Ofiesh
This is an 8x8 grid, so I am using Chess notation to indicate sqares.
Each diagonal from lower left
to upper right must contain the same number,
so the only thing to do is place one of the 0s in a diagonal that does not
start any numbers of more than 1 digit, except in some cases where placing a
0 in one diagonal may cause 0s to appear in another diagonal, in these cases
both diagonals must follow this condition.
So, if I put a 0 on c1, 0s
appear only on e3, f4, g5, and h6. Since none of
these start numbers this is an answer.
There are only 10 possible
ways to position numbers in this grid according
to the conditions specified. The other 9 possibilities all yield at least
one number with more than 1 digit starting with 0.
The other 9 possibilites yield
a 0 in the following locations, a8, a7, a6,
d8, a4, a3, a2, a1, and f5.
Starting with a 0 on c1 yields
the only possible answer.
Carl Strohmenger
The solution starts with a '1' in the upper left hand corner. This
results in no zeros beginning any entry, and with at least one entry
beginning with each of the digitd 1 through 9. If the upper left hand
corner contained any digit other than '1', then some other entry would
have to begin with zero, but that is not allowed by the rules. Thus the
solution is unique. Nice puzzle!
Toon Krijthe
Why is it unique:
First each number has digits
in consecutive increasing order. So the first
number determines all others:
1) A[x+1,y] = (A[x,y] + 1 ) mod 10
2) A[x,y+1] = (A[x,y] + 1 ) mod 10
According to this rule there are 10 solutions.
But the second rule states that no number can be started with a 0, this
eliminates 9 of these solutions,
leaving just one. And that one is unique.
Mark J Tilford also sent an answer.