
Tessellations
Patterns covering the plane by fitting together replicas of the same basic shape have been created by Nature and Man either by accident or design. Examples range from the simple hexagonal pattern of the bees' honeycomb or a tiled floor to the intricate decorations used by the Moors in thirteenth century Spain or the elaborate mathematical, but artistic, mosaics created by Maurits Escher this century. These patterns are called tessellations.
What is a tessellation?
In geometrical terminology a tessellation is the pattern resulting from the arrangement of regular polygons to cover a plane without any interstices (gaps) or overlapping. The patterns are usually repeating. There are three types of tessellation.
Regular Tessellations
Regular tessellations are made up entirely of congruent regular polygons all meeting vertex to vertex. There are only three regular tessellations which use a network of equilateral triangles, squares and hexagons.
Those using triangles and hexagons-

Semi-regular Tessellations
Semi-regular tessellations are made up with two or more types of regular polygon which are fitted together in such a way that the same polygons in the same cyclic order surround every vertex. There are eight semi-regular tessellations which comprise different combinations of equilateral triangles, squares, hexagons, octagons and dodecagons.
Those using triangles and hexagons-
Non-regular Tessellations
Non-regular tessellations are those in which there is no restriction on the order of the polygons around vertices. There is an infinite number of such tessellations.
Taking account of the above mathematical definitions it will be readily appreciated that most patterns made up with one or more polyiamonds are not strictly tessellations because the component polyiamonds are not regular polygons. The patterns might more accurately be called mosaics or tiling patterns. Regular tessellations in the mathematical sense are possible, however, with the moniamond, the triangular tetriamond and the hexagonal hexiamond. Semi-regular tesselations are possible with combinations of the moniamond and the hexagonal hexiamond. Nevertheless I will apply the term tessellation (as other authors have) to describe the patterns resulting from the arrangement of one or more polyiamonds to cover the plane without any interstices or overlapping.
The following definitions and descriptions refer to tessellations of polyiamonds. Examples are restricted , with some noteable exceptions, to tessellations of individual polyiamonds.
Tessellations can be created by performing one or more of three basic operations, translation, rotation and reflection, on a polyiamond (see Figure).

Translation - sliding the polyiamond along the plane. The translation operation can be applied to all polyiamonds.
Rotation - rotating the polyiamond in the plane. The rotation operation can be applied to all polyiamonds which do not possess circular symmetry, for example the hexagonal hexiamond, which remains unchanged following rotation through 60o or multiples thereof.
Reflection - reflecting the polyiamond in the plane, as if being viewed in a mirror. The reflection operation is limited to polyiamonds which are enantiomorphic. An enantiomorphic polyiamond is one which cannot be superimposed on its reflection, its mirror image.
I propose the following classification of polyiamond tessellations which is based on the operations performed on the polyiamond being tessellated..
Simple tessellations are those in which only the translation operation is used.
Complex tessellations are those in which one or both of the rotation and reflection operations is used with the translation operation.
A single or multiple of a polyiamond may be combined to form a figure which is capable of tessellating the plane using only the translation operation. This figure will be called the unit cell.
A particular unit cell may be filled by multiples of different polyiamonds. Gardner described how five pairs of heptiamonds could be used to fill the same unit cell tessellation pattern. You will be able to find many other examples in the illustrations later.
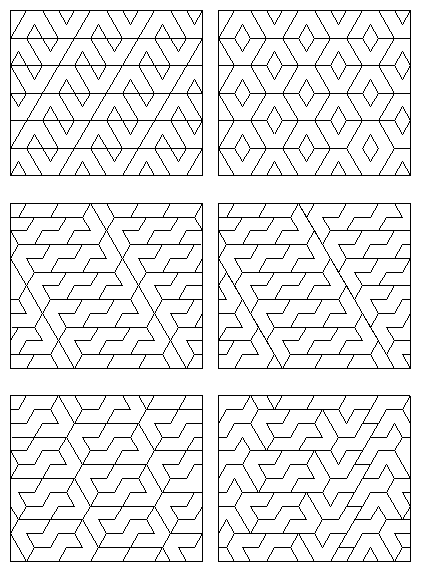
Tessellations may be further classified according to how the unit cells containing one or more polyiamonds are arranged. If the unit cells are arranged such that a regular repeating pattern is produced the tessellation is termed periodic. If the arrangement produces an irregular or random pattern the tessellation is termed aperiodic. Another arrangement which produces a tessellation with a centre of circular symmetry is termed radial - such tessellations, with the exception of special cases, are complex and will comprise two three or six unit cells each containing an infinite number of poyiamonds.
All tesselations which are regular belong to a set of seventeen different symmetry groups which exhaust all the ways in which patterns can be repeated endlessly in two dimensions.
The reader should realise that polyiamonds of odd order cannot provide simple tessellations. Every polyiamond of odd order is by definition unbalanced. The rotation and reflection operations must be used in order to provide balanced unit cells for tessellation.
All of the polyiamonds of order eight or less, with the exception of one of the heptiamonds will tessellate the plane. The exception is the V-shaped heptiamond. Gardner (6th book p.248) posed the problem of identifying this heptiamond and reproduced an impossibilty proof of Gregory. However, in combination with other heptiamonds or other polyiamonds, tesselations using this V-shaped heptiamond can be achieved.