

Ed Pegg Jr., March 28, 2005
At a family gathering a few years back, I taught the game of Go to a young nephew. In the space of a few hours, he learned the rules, various tools of strategy, and applications of that strategy. He recognized the traps I set for him in a series of quick demonstration games. Then we played a 13-stone handicap game on a 9x9 board, and he beat me.
In math instruction, one learns the rules, various tools of strategy, and applications of that strategy. Students learn to recognize common traps within a series of demonstrated problems. Notice the parallels here. Could abstract games work as part of a school curriculum? Historically, outside of Go and Chess, there haven't been many books on abstract games. That started changing in 1959 with Martin Gardner's column "The Game of Hex". He followed with "Bridg-it and other Games" in 1966. Donald Knuth got into the act in 1974 with Surreal Numbers, in tandem with John Conway's On Numbers and Games. Berlekamp, Conway, and Guy then put out Winning Ways in 1982.
Let's start with the Game of Hex. Players Black and White alternate turns placing a piece of their color inside a hexagon, claiming that hexagon. Black's goal is to form a black path connecting the black sides of the parallelogram, and White's goal is to form a white path connecting the white sides. Using Hex, Gardner demonstrated one frequent weakness of connection games, the point-pairing scheme. In the first diagram, White can always win by playing the paired cell to any move Black makes. I give a puzzle in the second diagram. White will use the given point-pairing scheme, after the first move. Black to move and win. For more on Hex, see Hex Strategy: Making the Right Connections by Cameron Browne.
 |
 |
The simplicity of connection games allows them to be easily learned. Their clarity and depth allows our human minds to understand them better than any computer system. I suppose that's why I like them so much. After being taught multiplication, how do you feel when a computer is shown effortlessly multiplying 100-digit numbers? Now look at a particular set of game rules, and proveto yourself your superiority over any computer on the planet. Which is better?
There is now a book covering these games we humans so excel at: Connection Games: Variations on a Theme by Cameron Browne (same guy as above). I'll quote myself off the back cover: "This is a great book. Every page of Connection Games works well, making it a classic work in an area that needed one. This would be an excellent book for motivating a person to like mathematics." That motivation, in my mind, comes from a young adult realizing just how fantastically intelligent they are, compared to some machine.
Since I'm mentioning machines, it helps to have a program that plays these games.
Zillions of Games is a computer gaming engine for Windows PCs that debuted in 1999. The engine can take any set of rules and play a game. For example, take a look at the ZRF file for Thai Chess. The "program" is actually a list of rules that define the game. Once the ZRF file is created, the system's artificial intelligence can automatically play one or more players. So far, over 1000 games and 5000 variants have been created by hobbyists and board game enthusiasts. Some of these games are educational (particularly those by Karl Scherer) and can be used in school classes to teach mathematics and other subjects. The developers of Zillions claim that the power of playful learning is significantly underestimated by some educators. It's a great deal at $25.
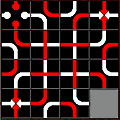
Many of the games in Connection Games are available in the Zillions of Games connection games list. I present them here, along with links to more information on each game.
|
 |
|
|||||||
|
 |
|
|||||||
|
 |
|
|||||||
|
 |
|
|||||||
|
 |
|
Zillions isn't all that great at connection games versus a human opponent. With a chess variant, or almost any other type of game, it plays very strongly. So, if you're disappointed with the play of some of these games, it's not that Zillions is bad, it's because you're brilliant. One demonstration of this was the Ing Challenge: a $1.6 million reward for the first computer program to defeat a strong amateur player at Go. No attempt was ever made to claim this prize. Notice that's for an amateur player. That's you, after a few hundred games against good opponents.
With many connection games, you can find further information at Richard's PBeM Server. You can also find human players there, along with an archive of games. Here is an example of one hard-fought game:
Lines of Action. andidi vs johnbosley
1. D1-B3 H5-F7 2. B3-F7 A3-C3 3. F1-F4 A7-C5 4. B1-D3 H3-E3 5. E1-G3 H7-F7
6. G1-G4 H6-F6 7. G4-E6 A6-D6 8. D3-D6 H4-E7 9. C1-D1 A2-E6 10. F4-D4 A5-C7
11. D1-D5 A4-A5 12. C8-E6 A5-D5 13. B8-B7 H2-G2 14. E6-D7 F6-D6 15. G3-D6 E3-F4
16. B7-C8 G2-G4 17. D6-E6 C7-E5 18. C8-B7 G4-F3 19. D4-F4 C5-D4 20. B7-C8 D5-F5
21. F4-G5 D4-D7 22. D8-C7 C3-B4 23. C7-E5 E7-G5 24. E5-F6 G5-G7 25. C8-C7 F3-G3
26. C7-E5 G3-H4 27. G8-D8 F5-G6 28. F8-C8 H4-F4 29. C8-C7 B4-B3 30. E5-D5 F4-D6
31. E8-C8 G7-C7 32. E6-E7 C7-E5 33. C8-E8 D7-E6 34. D5-C6 Resign
More on Lines of Action: an article by Ralph Betza, originally in an issue of NostAlgia. This gives a hint of how deep the game is.
The rules of LOA are: There are two players, Black and White, who play alternately. Black moves first. The initial position has Black men on b1-g1 and b8-g8, White a2-a7 and h2-h7 (12 pieces each). The object of the game is to connect all your pieces into one group. Two men form a connected group if they are on adjacent squares (that is, if one of the men were a chess King, it would be able to move to the square occupied by the other). The men may move in any of the 8 directions (the same directions as a chess King or Queen). The peculiarity of this game is that the number of squares a man may move in a given direction is determined by counting the number of men of either color along that line of action. Example: in the initial position, legal first moves are 1. b1-b3, c1-c3, d1-d3, etc. b1-h1, g1-a1, b1-d3, c1-e3, d1-f3, e1-g3, f1xh3, et cetera (and the symmetrically equivalent moves of the 8th rank men). Note that in the example we have introduced two new rules: you may move through your own men, but not through your opponent's men; you may capture an opponents man by moving to the square it occupies, but you may not capture your own men. A few example moves: 1.d1-b3,h3-e3 2.b3xe3,h6xe3 3.c1xe3,a7-d4 4.g1xd4,a4xd4 5.e1-e4,h7-e4 and we will return to this position in later discussions. One last rule: if the move which unites your men unites your opponent's men (by capturing his last isolated man) the game is drawn. Stalemate is almost impossible in an actual game.
Before I discuss the new ideas of LOA strategy which I have developed, I will summarize the thinking of the classical school. Most of the classical ideas are at least partially valid, and the technical terms introduced are still needed.
CLUMPS this refers to the number of disconnected units (groups or single men) had by each side. In the initial position each side has two clumps, but after the normal opening move 1.d1-b3 Black has 4 clumps. Since the object of the game is to have only one clump it seems logical that the less clumps you have the better off you are. Actually, this has little practical application, and players who habitually count clumps often reject good moves which increase their clumpcount.
COUNTING "It takes him 5 moves to connect, but I can do it in 4," says the classical player to himself, and he rushes to connect, having considered as possible defenses only the other player's connection attempts. This is because the classical player sees LOA as a race to connect. When his opponent calmly sets up a deadly blocking move or a capture that cuts the classicist in two, the classicist does not learn his lesson, but merely curses his luck.
CAPTURES "The less pieces you have, the less pieces you have to connect" says the old school, and therefore believes that captures are to be avoided. In fact, the more pieces you have, the more men you have to block with, the more mobility you have, and further the more men you have to connect WITH!
LENGTH if you think of the game as a race, it is natural to think that long moves are better than short ones. This idea has some validity, but important moves count for more than aimless long ones. In fact, it is often good to move a man one space in the opening because it creates flexibility.
CROSS-RUSH is the classic racing strategy, seen in the example game above. The idea is to leave one of your original clumps at home while the other 6 men run swiftly across the board to join it. As you see above, the runners try to get themselves captured in order to reduce the number of men that have to make the trip. The cross-rush is a losing strategy because of the "weakness of the original position." In the above example a winning plan for W would be a5-c7,h5-f7,a2-d5,f7-d7,d4xd8 or similar ideas.
CENTRAL BLOCK is the strategy of advancing into the center from both sides in order to unite there. Presumably the opponent will find it hard to connect around the outside of your block. This is essentially the correct strategy of LOA, except that the classical ideas of "center" and of "block" are too narrow.
BRIDGE is a lovely strategy which can't be forced. The idea in its simplest form is to move men from both your original clumps, preferably from the ends so you don't split the original clumps into too many pieces, and form the men into a long, thin chain which stretches from one side of the board to the other and connects your groups. It is possible to connect in 6-10 moves with this strategy.
Browne devotes a third of Connection Games to definitions, properties, classification, and strategy. More than a half is devoted to the games themselves, sort of a Hoyle's book of Connection Games. His researches revealed that Hex (1942) wasn't the first connection game -- that honor belongs to Lightning, which was patented in 1892 by H. Doty. Among the discussions in the rest of the book are graph theory and tessellations, two topics any young adult should know. Every page has beautiful, pertinent illustrations of the games in question.
A few games in particular deserve an extra mention here. Kaliko and Tantrix are both beautiful games. Amazons is one of my favorite games, even though it is more of a game of detaching your opponent from territory. Gonnect is likely the best of all connection games. Star and Y are both available from Kadon.
Browne closes Connection Games with the following words: There are strong indicators that simply playing board games in general improves children's mathematical skills. Hallett [2003] describes how fifth-grade students encouraged to play board games performed significantly better at a statewide mathematics test than students of previous years -- and had a lot of fun along the way.
It's not just the young that benefit. Brain health benefits from many activities, one of them being puzzles and games. If you want to keep your brain sharp, try a connection game with a friendly human. You'll be making calculations in your mind that no computer on earth can compete with.
Elwyn R. Berlekamp, John H. Conway, and Richard K. Guy, Winning Ways for Your Mathematical Plays, AK Peters, Ltd., 2001.
Cameron Browne, Connection Games: Variations on a Theme, AK Peters, Ltd., 2005.
Cameron Browne, Hex Strategy: Making the Right Connections, AK Peters, Ltd., 2000.
David Eppstein, "Combinatorial Game Theory," http://www.ics.uci.edu/~eppstein/cgt/.
Martin Gardner, "The Game of Hex," Mathematical Puzzles and Diversions, Simon & Schuster, 1963.
Walter Joris, 100 Strategic Games For Pen And Paper, Carlton Books, 2002.
Mark Lefler and Jeff Mallett, Zillions of Games, http://www.zillions-of-games.com/.
Mindy McAdams, How to Teach Go, http://www.sentex.net/~mmcadams/teachgo/.
Richard J. Nowakowski, Games of No Chance, Cambridge University Press, 1998. http://www.msri.org/publications/books/Book29/contents.html.
Richard J. Nowakowski, More Games of No Chance, Cambridge University Press, 2002. http://www.msri.org/publications/books/Book42/contents.html.
Alex Randolph, "40 Twixt puzzles," http://www.gamerz.net/pbmserv/Twixt/puzzles.html.
Eric W. Weisstein. "Game of Hex." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/GameofHex.html.
Wikipedia, Hex (board game), http://en.wikipedia.org/wiki/Hex_(board_game).
Comments are welcome. Please send comments to Ed Pegg Jr. at ed@mathpuzzle.com.
Ed Pegg Jr. is the webmaster for mathpuzzle.com. He works at Wolfram Research, Inc. as an associate editor of MathWorld, and as administrator of the Mathematica Information Center.