Chebychev Polynomials were used by Bill
Daly and
Steven Stadnicki to solve
a problem. I've built a TRIANGLE
page for the results, with new contributions by Bob
Harris,
Roger Phillips, and many
others.
The MacTutor
History of Mathematics archive gives Pafnuty
Lvovich Chebyshev's biography. At mathworld.wolfram.com,
there are twenty different entries for Chebyshev, including Chebyshev
Polynomial of the First Kind and Chebyshev
Polynomial of the Second Kind. What do they mean? I gained
my first insight when I plugged cos(Pi/9) into the Inverse
Symbolic Calculator. The Sixth Chebyshev Polynomial of the Second
Kind is -1 + 24 x2 - 80 x4 + 64 x6.
In Mathematica, ChebyshevU[6,x]. This polynomial is also expressed
as U6(x).
ChebyshevU[6,x] = -1 + 24 x2 - 80 x4 + 64
x6 = - (1 + 4 x - 4 x2 - 8 x3) (1 - 4
x - 4 x2 + 8 x3)
-(1 + 4 x - 4 x2 - 8 x3) / 8 = (x - cos(2p/7))
(x - cos(4p/7)) (x - cos(6p/7))
(1 - 4 x - 4 x2 + 8 x3) / 8 = (x - cos(p/7))
(x - cos(3p/7)) (x - cos(5p/7))
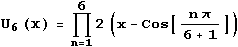Thus, this polynomial is closely related to the heptagon. Similarly,
1 - 6 x + 8 x3 is closely related to the nonagon, as a factor
of U8(x). In general, the following is true
... but I don't see at Mathworld, or in my references.
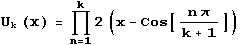Please visit the Mathworld link (Chebyshev
Polynomial of the Second Kind) to see more representations. A
useful recurrence relationship: U0(x) = 1. U1(x)
= 2x. Uk+2(x) = 2 x
Uk+1(x) - Uk(x).
This is easily proved by induction if you use the matrix representation,
but would likely be tricky using the product of cosines relationship.
