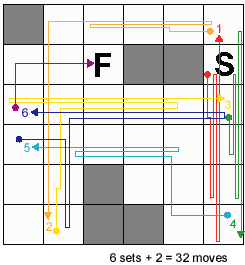
I've just had a look at last week's mazes. Andrea's is excellent. The
shortest path, divided into groups of 5 moves by commas, seems to be
ddudu, llr (or ddu) ld, uurlr, dudud, lulrl, rdurl, ur which is 32
steps.
Chris Lusby Taylor

Hi! I like the 12345 maze.
My Answer of Andrea's 12345 maze is 32 moves shown by the attached file.
I enjoyed.-Koshi Arai

Here's the solution to Andrea's 12345 maze:
S1-S2-N3-S4-N5
S1-S2-N3-W4-S5
N1-N2-E3-W4-E5
S1-N2-S3-N4-S5
W1-N2-W3-E4-W5
E1-S2-N3-E4-W5
N1-E2
Pretty good maze.

-- Bob Abbott

Andrea's maze:
DDUDU WWEWD UUEWE DUDUD WUWEW EDUEW UE
JP Ikäheimonen

Surprisingly tricky for such a simple-appearing maze... 32 moves:

1 2 3 4 5
D D U D U
D D U L D
U U R L R
D U D U D
L U L R L
R D U R L
U R

Linear in the sense that there was only one place to take the '5' move
in each case, if moves back to a previous '5' location are disallowed.

Tim Firman

I finally solved Andrea Gilbert's 12345 maze by back-solving the last
several steps.

The finish can only be reached by a 1 or 2 move.

A 1 move must have been preceded by a 5 move, which must end at an edge of
the board in a line with no blockers. (Note that there are only 4 such
lines, so only 8 such states to consider, or 9 if you include the start
state.)

None of the spaces 1 away from the finish fits this description, so the
finish must be reached by a 2 move, which was preceded by a 1 move from one
of the 9 states mentioned above. Only one pair of last two moves allows
this: Up 1, Right 2.

The two moves before that could only be Right 4, Left 5.

The next previous move could have been Left 3 or Up 3. However, there is no
1-2 path from a start-or-after-5-move state that could lead to the Left 3
move, and only one for the Up 3 move, so the next 3 previous moves were
Right 1, Down 2, Up 3.

This was a state I had reached going forward, so the maze was solved.

Down 1, Down 2, Up 3, Down 4, Up 5
Left 1, Left 2, Right 3, Left 4, Down 5
Up 1, Up 2, Right 3, Left 4, Right 5
Down 1, Up 2, Down 3, Up 4, Down 5
Left 1, Up 2, Left 3, Right 4, Left 5
Right 1, Down 2, Up 3, Right 4, Left 5
Up 1, Right 2

An interesting way to think of this is a 6 move solution in a maze with 9
states. The moves are just complicated (like in the cooperation maze,
except there, you have a long path of complicated moves -- and no, I haven't
solved the new one yet).

The solution visits 7 of the possible 9 states. The other two states, as it
turns out, are unreachable, although one of them could be reached if the
start square was elsewhere.

I also solved the non-euclidean maze. Tricky, but not entirely different
than some game maps I've seen. Once I figured out that the distorted
perspective was only a distraction, it wasn't too hard, though it still took
me a while to find my way to the second green room.

/dev/joe

Very nice maze.

+-----+-----+--------------------------+
|xxxxx|9    |     |     |     |5,8,19  |
+-----+-----+-----+-----+-----+--------+
|31   |     |F,32 |xxxxx|xxxxx|S,3,6,17|
+-----+-----+-----+-----+-----+--------+
|14,30|12,28|     |     |13   |1,15,29 |
+-----+-----+-----+-----+-----+--------+
|25   |23,26|     |     |22   |7,16,24 |
+-----+-----+-----+-----+-----+--------+
|     |  11 |xxxxx|     |     |2,18    |
+-----+-----+-----+-----+-----+--------+
|     |10,27|xxxxx|xxxxx|21   |4,20    |
+-----+-----+-----+-----+-----+--------+

Thanks,
Carl

Here we go:
(U)p (D)own (L)eft (R)ight
1 2 3 4 5
D D U D U
L L R L D
U U R L R
D U D U D
L U L R L
R D U L R
U R

I think that does it. ::)
-Matt Elder